Электрические двигатели в регулируемых электроприводах. Двигатели постоянного тока. Ограничения, накладываемые на режимы преобразования энергии в машинах постоянного тока, страница 10

Угол между осями обмоток равен 2p/3. Поэтому 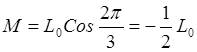. Следовательно, .

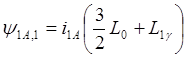Здесь 3/2L₀=L₁₂ представляет собой результирующую индуктивность, обусловленную магнитным потоком в воздушном зазоре (главным потоком), создаваемым суммарным действием токов статора; L₁₂+L_1g=L₁ – эквивалентная индуктивность обмоток статора. Тогда:

y_1А,1=L₁i_1A.

Так как машина симметрична, то

y_1В,1=L₁i_1В,

y_1С,1=L₁i_1С.

Каждая обмотка ротора создает в воздушном зазоре потокосцепления L₀i’_2А, L₀i’_2В, L₀i’_1C. Если угол между одноименными осями обмоток статора и ротора равен q₂, то с учетом того, что угол между осями обмоток равен 2p/3, результирующие потокосцепления обмоток статора, обусловленные совместным действием токов статора и ротора, получим в следующем виде:

,

,

.

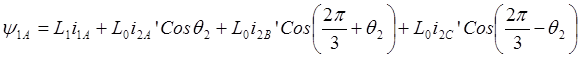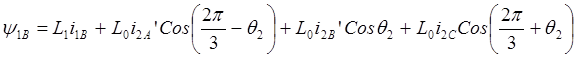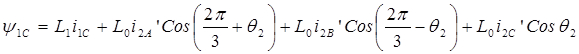Следовательно, в неподвижной системе координат (в осях a,b) результирующий вектор потокосцепления запишется следующим образом:

.

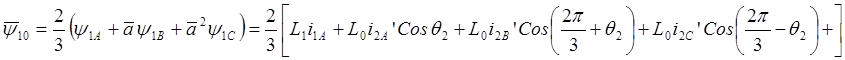
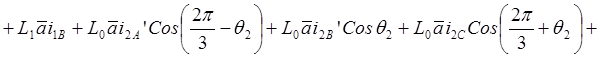
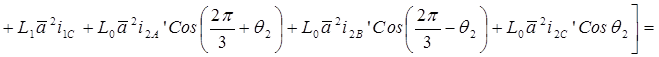
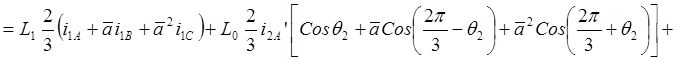
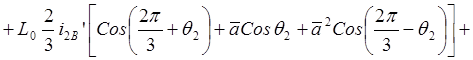
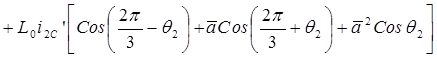После преобразования получим:

.

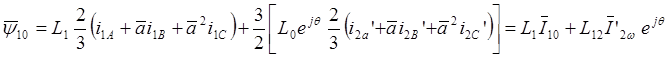Здесь результирующий вектор I₁₀ соответствует неподвижной системе координат, а вектор I’₂w - системе координат, вращающейся со скоростью вращения ротора.

В соответствии с выражением (2.4) вектор представляет собой результирующий вектор тока ротора в неподвижной системе координат:

Следовательно,

.                     (2.17)

Аналогичным образом для вектора потокосцепления ротора в неподвижной системе координат можно получить выражение

.                     (2.18)

Раскладывая векторы y y по осям a, b получим:

,

,                     (2.19)

,

.

Учитывая выражения (2.3), (2.4), результирующие веторы потокосцеплений статора и ротора можно представить во вращающейся системе координат X, Y в следующем виде:

,                (2.20)

.

Тогда:

,

,                     (2.21)

,

.

В системе координат, вращающейся с произвольной скоростью w_к=const, векторы можно представить в следующем виде:

,

(2.22)

.

2.9  Электромагнитный момент.

Энергия, потребляемая двигателем от источников питания, частично теряется в активных сопротивлениях обмоток и расходуется на создание магнитного потока. Оставшаяся часть энергии затрачивается на выполнение механической работы.

Мгновенная мощность, потребляемая двигателем со стороны статора, определяется мгновенными значениями напряжения питания и токов статора:

.

С учетом того, что в неподвижной системе координат:

u_1A=u_1a, , ,

i_1A=i_1a, , ,

Находим: .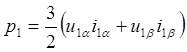

Так как ,, полученное выражение для мощности потребления статорной цепи можно описать следующим образом: ,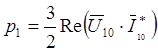

Где  – вектор, сопряженный вектору .

Справедливость последнего выражения можно подтвердить непосредственным вычислением:

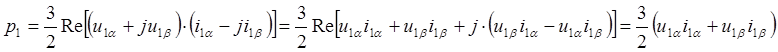Скалярное произведение векторов определяется значениями их модулей и углом между векторами, но не зависят от того, в какой системе координат они представлены (произведения векторов инвариантно по отношению к системе координат), так как в разных координатных системах взаимное расположение векторов не меняется. Следовательно, если результирующие векторы напряжений питания статора и токов статора в любой системе координат обозначить через ,  то всегда:

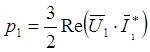
в том числе в системе координат, вращающейся со скоростью вращения магнитного поля,

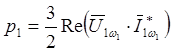
и в системе координат, вращающейся с произвольной скоростью w_к=const:

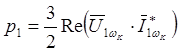
Для машины двойного питания, получающей энергию так же со стороны ротора, аналогичным образом можно показать, что мгновенная мощность, потребляемая двигателем со стороны ротора, определяется выражениями:

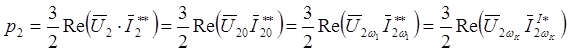
Следовательно, общая мощность, потребляемая двигателем равна:

.

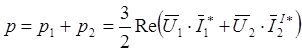В дальнейшем ограничимся рассмотрением процессов асинхронного двигателя, не получающим энергию со стороны ротора. Тогда:

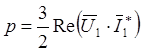.                     (2.25)

Используя уравнение баланса напряжений в статорной цепи и уравнения связи между потокосцеплениями и токами уравнения (2.25) можно получить в разных формах. Наибольшее распространение получили выражения, в которых в качестве переменных могут быть использованы следующие комбинации векторов: . При этом в каждой из комбинаций результирующие вектора должны описываться в одной и той же системе координат.