Электрические двигатели в регулируемых электроприводах. Двигатели постоянного тока. Ограничения, накладываемые на режимы преобразования энергии в машинах постоянного тока, страница 5

T_вт = L_м/R_вт, T_вм = (L_в+L_м)/R_в

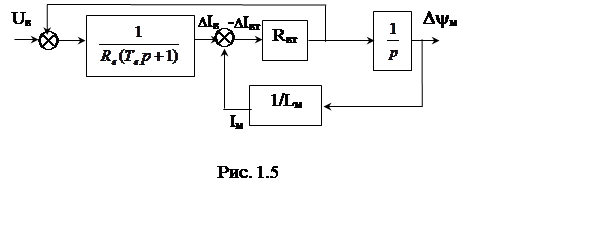
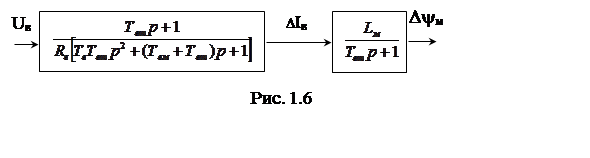
В системах подчиненного регулирования в качестве типовых моделей объектов управления рассматриваются модели первого порядка. Переход от модели второго порядка (рис. 1.6) с передаточной функцией W_в(р)=DI_в(р)/DU_в(р) к модели первого порядка можно осуществить разными способами.

 

В первом случае «усечение» передаточной функции W_в(p) путем отбрасывания в знаменателе слагаемого ТвТ_втр². Вносимая при этом погрешность аппроксимации W_в(р) находится в допустимых пределах, если соблюдается равенство:

(1-Т_втТ_вw²)²+(Т_вм+Т_вт)²w²= 1+(Т_вм+Т_вт)²w²

или

-2Т_вТ_втw²+(Т_вТ_втw²)²=0.

Следовательно, если частота среза интересуемой системы не превышает значения 2/Т_вТ_вт, то рассматриваемое упрощение допустимо.

Второй вариант основан на том, что решение характеристического уравнения

Т_вТ_втр²+(Т_вм+Т_вт)р+1=0

являются вещественными, вследствие чего

Т_вТ_втр²+(Т_вм+Т_вт)р+1 = (Т_в1р+1)(Т_в2р+1)

при Т_в1>>Т_в2 [13]. В этом случае можно принять:

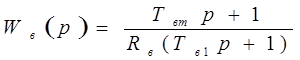Следует заметить, что параметры линеаризованной модели цепи возбуждения (рис. 1.6) существенным образом зависят от выбора рабочей точки, относительно которой производится линеаризация, и изменяются в широких пределах. Однако, как показано [13], при изменении параметров их соотношения сохраняются такими, что частотные характеристики модели (рис. 1.6) при выборе различных рабочих точек изменяются незначительно, вследствие чего изменениями параметров в большинстве случаев можно пренебречь.

Полученные модели могут быть положены в основу систем регулирования ЭДС генераторов постоянного тока и угловой скорости вращения двигателей с независимым возбуждением. При этом в качестве рабочей точки, относительно которой производится

линеаризация нелинейной зависимости целесообразно выбирать точку при y_м<y_м,н, где y_м.н – потокосцепление в номинальном режиме.

При выполнении практических расчетов более удобно может оказаться применение схемы на рис. 1.6 в несколько видоизмененной форме (рис. 1.7), где К_ф=L_м/v. В этом случае коэффициент К_ф можно определить непосредственно по кривой намагничивания Ф=Ф(I_в).

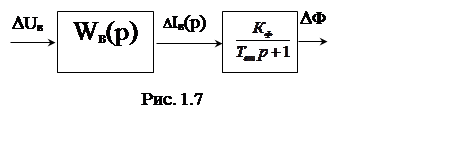Следует заметить, что для машин малой и средней мощности, магнитопроводы которых выполняются шихтованными, можно принять: Т_вт=0.

1.5  Структурная схема двигателя с независимым возбуждением.

В регулируемых электроприводах в качестве регулируемых источников питания якорных цепей двигателей могут быть использованы машинные или полупроводниковые преобразовательные агрегаты. Для случая применения машинных преобразователей, реализуемых как правило, на основе генераторов с независим возбуждением, и реверсивных полупроводниковых преобразователей ток якоря может протекать в любом направлении, зависящем от работы двигателя. Тогда схему замещения якорной цепи можно представить в виде генератора противо-ЭДС (рис. 1.8). здесь Е_п – ЭДС преобразовательного агрегата, R_а, L_а – параметры якорной цепи, Е – противо-ЭДС, вырабатываемая якорной цепью двигателя. В составе R_а, L_а учитываются активные сопротивления и индуктивности всех обмоток, включенных в якорную цепь двигателя (компенсационная обмотка, обмотка добавочных полюсов), и сопротивления и индуктивности преобразовательного агрегата.

Предполагается, что параметры R_a, L_a неизменны (R_a рассчитывается, как правило, для нагретого состояния машин), а влияние реакции якоря на возбуждение двигателя отсутствует.

(1.5)

 При принятых условиях якорная цепь описывается следующими уравнениями:

Е = СФw               

здесь С – конструктивная постоянная двигателя [5], Ф – магнитный поток, создаваемый обмоткой независимого возбуждения, w - угловая скорость вращения якоря.

Уравнения (1.5) необходимо дополнить выражением, описывающим формирование электромагнитного момента, и уравнением движения: