Электрические двигатели в регулируемых электроприводах. Двигатели постоянного тока. Ограничения, накладываемые на режимы преобразования энергии в машинах постоянного тока, страница 11

Учитывая инвариантность скалярных произведений векторов к системе координат, для вывода выражений, описывающих развиваемый двигателем электромагнитный момент, можно выбрать один конкретный вариант системы координат.

В качестве базового варианта выберем систему координат X,Y, вращающуюся со скоростью вращения магнитного поля. Тогда:

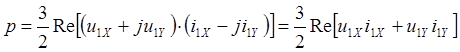         (2.26)

Подставляя в (2.26) значения напряжений из (2.9), получим следующее выражение:

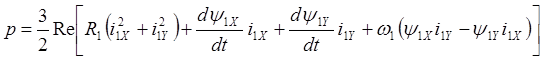
Здесь слагаем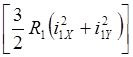ое  представляет собой типовые потери в обмотках статора, а слагаемое 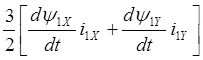– мощность энергии. Характеризующей приращение запасаемой в индуктивностях статора электромагнитной энергии. Следовательно, мощность, передаваемая на вал электродвигателя (мощность в зазоре, электромагнитная мощность), равна

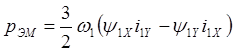.                  (2.27)

Здесь 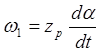, где Z_р – число пар полюсов, da - пространственный (геометрический) угол поворота ротора.

Механическая работа, выполняемая двигателем при повороте ротора на угол da, равна произведению развиваемого двигателем момента М на этот угол, т.е. W_мнх=М×da. Следовательно, электромагнитная мощность описывается выражением:

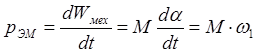                 (2.28)

Из равенства выражений (2.27) и (2.28) следует, что

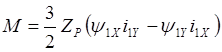.                 (2.29)

Полученной выражение можно представить в следующем виде:

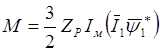.                    (2.30)

Идентичность выражений (2.29) и (2.30) можно проверить непосредственным вычислением.

Учитывая, что , выражение (2.30) перепишем следующим образом:

.

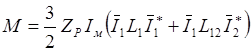Произведение  является вещественным числом. Следовательно,

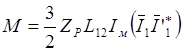                  (2.31)

Заменяя в (2.30) вектор , выражением 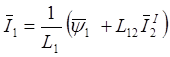 находим:

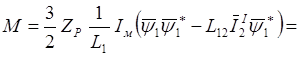
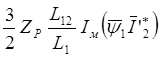.   (2.32)

Из (2.22) следует, что:

.

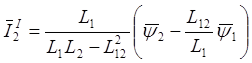следовательно,

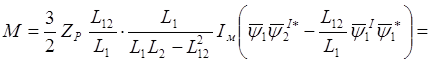
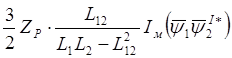 (2.33)

Подставляя в (2.33) выражение

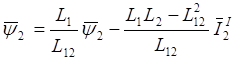, получаемое из (2.22), находим:

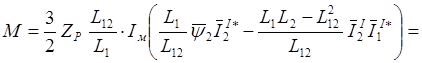
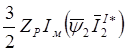           (2.34)

Так как: 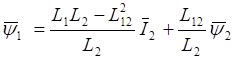, из (2.33) находим:

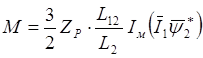.                      (2.35)

Выражения (2.30)-(2.35) представляют все возможные способы представления электромагнитного момента, развиваемого двигателем.

2.10  Структурная схема.

Как следует из уравнений состояния статора и ротора, а так же из уравнений, описывающих формирование потокосцеплений статора и ротора, следует, что асинхронный двигатель имеет внутренние перекрестные связи. Наиболее простая структурная схема двигателя, имеющая наименьшее количество перекрестных связей, получается при использовании базовой системы векторов y₁, y₂.

Рассматривая уравнения машины в неподвижной системе координат a,b из (2.17) и (2.18) находим:

,

,

,

,

,

.

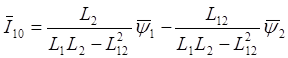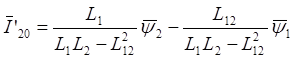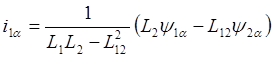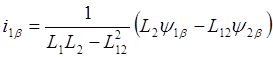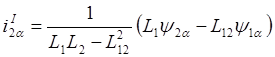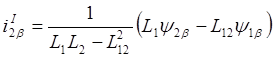Следовательно уравнения (2.6) и (2.13) можно преобразовать к виду:

,

,

,

.

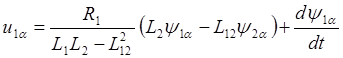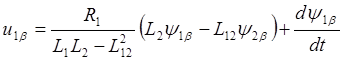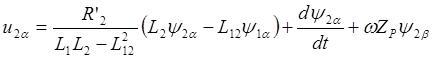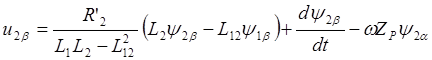Следовательно, динамические свойства асинхронного двигателя в осях a,b описываются уравнениями:

,

,

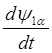
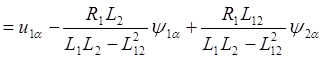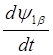
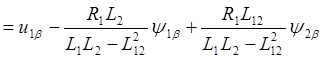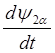
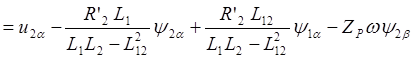,                (2.36)

,

,

.

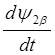
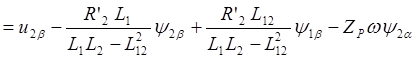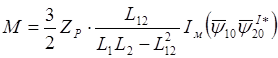
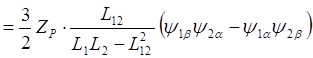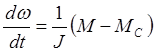Уравнениям (2.36) соответствует структурная схема электромеханического преобразования энергии в асинхронном двигателе, представленная на рис. 2.4.

Распространенным вариантом построения систем управления частотно-управляемым электроприводом является использование принципа какого-либо из результирующих векторов по вещественной оси системы координат.

Для случая ориентации вектора потокосцепления ротора по оси a имеем: y_2b=0, 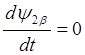, y_2a=|y₂|. Тогда система уравнений (2.36) упрощается:

,

,

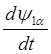
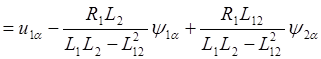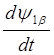
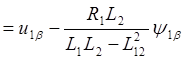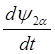
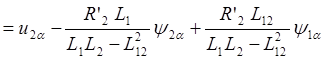,                        (2.37)

,

,

.

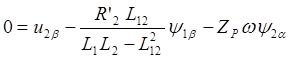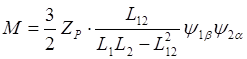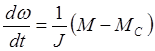Объединив второе и четвертое уравнения системы (2.37), можно получить структурную схему двигателя в этом частном случае (рис. 2.5).

При записи уравнений двигателя в осях X,Y получим систему уравнений:

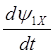
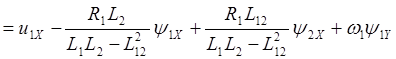
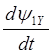
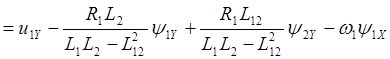
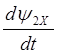
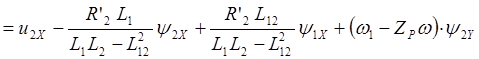            (2.38)

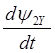
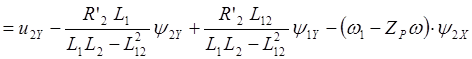
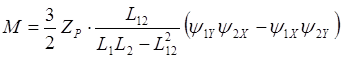
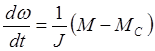
Соответствующая структурная схема приведена на рис. 2.6.

При ориентировании системы управления по потокосцеплеию ротора таким образом, чтобы обеспечивались условия y_2y=0, y_2х=const, убедимся, что в установившихся режима двигателей описывается уравнениями:

                               (2.39)

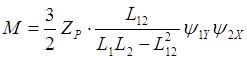
При отсутствии питания со стороны ротора U_2х=U_2y=0. Тогда i’_2x=0 и из второго и четвертого уравнений системы (2.21) находим:

,

 

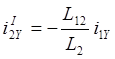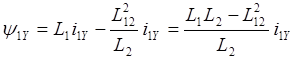
Следовательно,

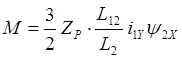
Полученное выражение показывает, что при совмещении вещественной оси х вращающейся координатной системы с вектором потоксцепления ротора управление моментом асинхронного двигателя подобно управлению моментом двигателя постоянного тока с независимым возбуждением.