Электрические двигатели в регулируемых электроприводах. Двигатели постоянного тока. Ограничения, накладываемые на режимы преобразования энергии в машинах постоянного тока, страница 18

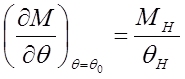
3.14  Регулирование скорости.

Основным способом изменения установившейся скорости вращения ротора является изменение частоты напряжения, питающего статорные цепи. При этом используются методы частотного управления, пригодные для управления асинхронным двигателем с некоторыми изменениями. Так, например, при частотно-токовом управлении отпадает необходимость в задании абсолютного скольжения b (следует принять b=0).

3.15  Устойчивость режимов работы двигателя.

При увеличении нагрузки на валу рабочий угол q увеличивается. В связи со склонностью синхронного двигателя к колебаниям переходный процесс изменения рабочего угла имеет значительно перерегулирования При этом превышение максимального значения q некоторого практического значения приводит к выпадению двигателя из синхронизма. Рассмотрим этот вопрос подробнее.

Начальному устойчивому режиму работы с некотоорым моментом на валу М₀ и рабочим углом q₀ соответствует точка а (рис. 3.7,а). При скачкообразном изменении момента сопротивления до величины М_С возникает переходный процесс. Так как перед началом переходного поцесса момент, развиваемый двигателем, был равен М₀, то для начального этапа переходного процесса управление движения ротора можно записать в следующем виде:

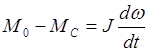                       (3.20)

Отсюда следует, что ротор начинает вращаться с отрицательным ускорением, абсолютное значение скорости снижается и становится меньше синхронной скорости, появляется положительное скольжение (рис.3.7,б), рабочий угол увеличивается.

За счет появления асинхронного момента (3.18) общий момент, развиваемый двигателем, превышает момент, определяемый выражением (3.16) на величину асинхронного момента. При этом рабочая точка будет перемещаться по кривой аб. В процессе этого движения момент, развиваемый двигателем, меньше момента сопротивления, вследствие чего происходит непрерывное снижение скорости и увеличение скольжения.

В точке б момент двигателя равен моменту сопротивления. Следовательно, уравнения движения примет вид:

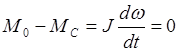
Снижение скорости вращения ротора прекратится. Но вследствие того, что w<w₁, рабочий угол будет увеличиваться и, в соответствии с (3.16), будет увеличиваться синхронный момент. При этом общий момент, развиваемый двигателем, также увеличится и превысит момент сопротивления. Следовательно, из уравнения движения:

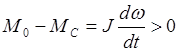
устанавливаем, что скорость двигателя начинает возрастать, а скольжение уменьшится. Со снижением скольжения уменьшается также и асинхронный момент и разность между полным моментом и моментом, определенным из (3.16), уменьшится.

В точке в скорость вращения ротора равна синхронной, но развиваемый двигателем момент превышает момент сопротивления, вследствие чего двигатель разгоняется выше синхронной скорости, скольжение и асинхронный момент отрицательны.

В точке г момент двигателя равен моменту сопротивления, и увеличение скорости вращения прекратится. Однако вследствие того, что w>w_1, рабочий угол будет уменьшаться, что приведет к снижению момента (3.16). Общий момент так же снизится, вследствие чего момент сопротивления превышает момент двигателя. Ротор начинает тормозиться.

Продолжая рассуждения, находим, что после затухания колебаний в точке д устанавливается новый режим, соответствующий моменту сопротивления М_С.

Если в переходном процессе изменения скорости и моментов рабочая точка попадает в точку в₁ (пунктирная линия), то М₁-М_С<0 и будет продолжаться снижение скорости и увеличение рабочего угла, двигатель выпадает из синхронизма. Следовательно, в переходном режиме рабочий угол не должен превышать критическое значение q_кр угла, определяемый точкой в₂ пересечения уровня М_С со спадающей ветвью угловой характеристики. Для создания необходимый запас устойчивости желательно, чтобы максимальное значение рабочего угла было меньше q_кр на p/30 … p/18.

Для оценки устойчивости переходных процессов можно использовать упрощенный метод площадей, который с использованием построений, приведенных на рис.3.8, можно сформулировать следующим образом: