Электрические двигатели в регулируемых электроприводах. Двигатели постоянного тока. Ограничения, накладываемые на режимы преобразования энергии в машинах постоянного тока, страница 6

(1.6)

М = СФi

здесь М_с – приведенный к валу двигателя момент сопротивления, J – приведенный момент инерции.

Момент сопротивления может содержать составляющие, сложным образом зависящие от скорости вращения или угла поворота вала двигателя. Каждая из составляющих и момент М_с в целом содержат и активные и реактивные компоненты. Реальный состав М_с определяется при рассмотрении конкретных процессов, для управления которыми используется двигатель. Точный учет влияния момента сопротивления реактивного характера рассмотрен в [13].

 

 

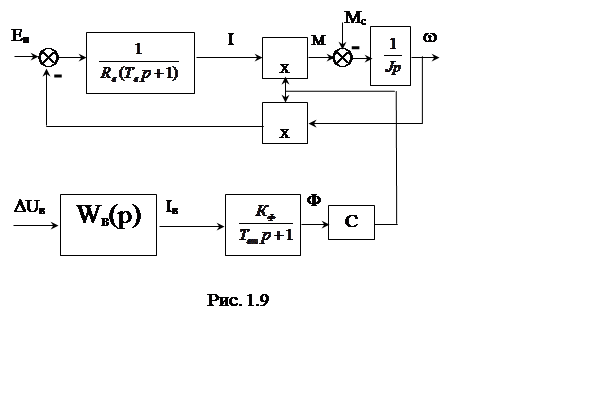
В общем случае систему уравнений (1.5), (1.6) необходимо дополнить уравнениями, описывающими формирование магнитного потока. Тогда полную структурную схему двигателя можно представить в виде рис. 1.9. Здесь, с учетом изложенного в п.1.4, опущены знаки отклонений для координат цепи возбуждения.

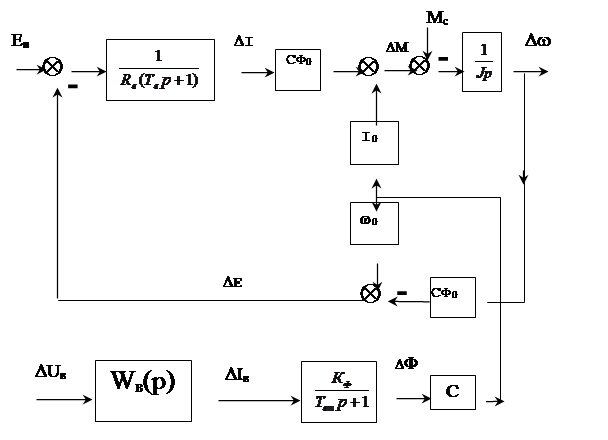
Полученная структурная схема характеризуется перемножением координат и является нелинейной. В некоторых вариантах электроприводов, (например, при одновременном изменении входных сигналов Е_п и U_в) полезной может оказаться линеаризованная модель структурной схемы. Линеаризация заключается в разложении нелинейных зависимостей в ряд Тейлора по степеням малых отклонений координат, входящих в произведения, и отбрасывании в этих разложениях нелинейных членов, представляющих собой члены высшего порядка малости.

Если для некоторого установившегося режима электромагнитный момент и ЭДС двигателя равны соответственно

                     М₀ = СФ₀I₀, Е₀ = СФ₀w₀,               (1.7)

то при отклонении потока, тока, и угловой скорости вращения соответственно на малые величины DФ, DI, Dw, то новые значения момента и ЭДС можно определить следующим образом:

М₀+DМ=С(Ф₀+DФ)(I₀+DI),

                    Е₀+DЕ=С(Ф₀+DФ)(w₀+Dw).               (1.8)              

Тогда

DМ = С(Ф₀+DФ)(I₀+DI)-СФ₀I = СФ₀DI+СI₀DФ+СDФDI

DЕ = СФ₀Dw+Сw₀DФ+СDФDw              (1.9)

Отбрасывая слагаемые второго порядка малости, получим:

DМ = СФ₀DI+СI₀DФ

DЕ = СФ₀Dw+Сw₀DФ                    (1.10)

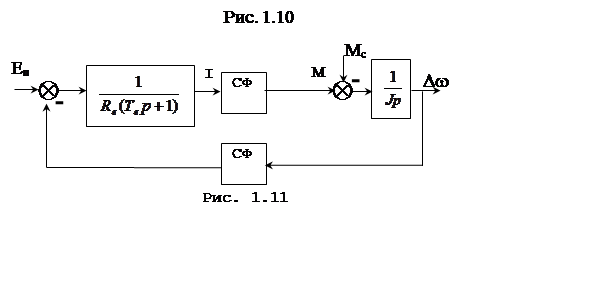
Следовательно, линеаризованную модель двигателя можно представить в виде схемы, приведенной на рис. 1.10.

При неизменном потоке возбуждения структурная схема двигателя упрощается (рис. 1.11)

1.6  Структурная схема двигателя с последовательным возбуждением.

Двигатели с последовательным возбуждением имеют, как правило, шихтованные магнитопроводы. Поэтому влиянием вихревых токов можно пренебречь. Тогда двигатель можно описать системой уравнений:

Е = СФw

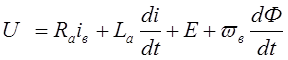М = Сфi                     (1.11)  

Ф = Ф(i) где v - число витков обмотки возбуждения.

Система уравнений (1.11) соответствует структурная схема, приведенная на рис. 1.12.

После замены кривой намагничивания линейной зависимостью Ф=k_фi получаем упрощенную схему, показанную на рис. 1.13.а. при моделировании более приемлемой может оказаться схема, приведенная на рис. 1.13.б.

Узлы вычисления момента и ЭДС можно линеаризовать аналогично линеаризации соответствующих узлов двигателя с независимым возбуждением согласно выражению (1.10).

 

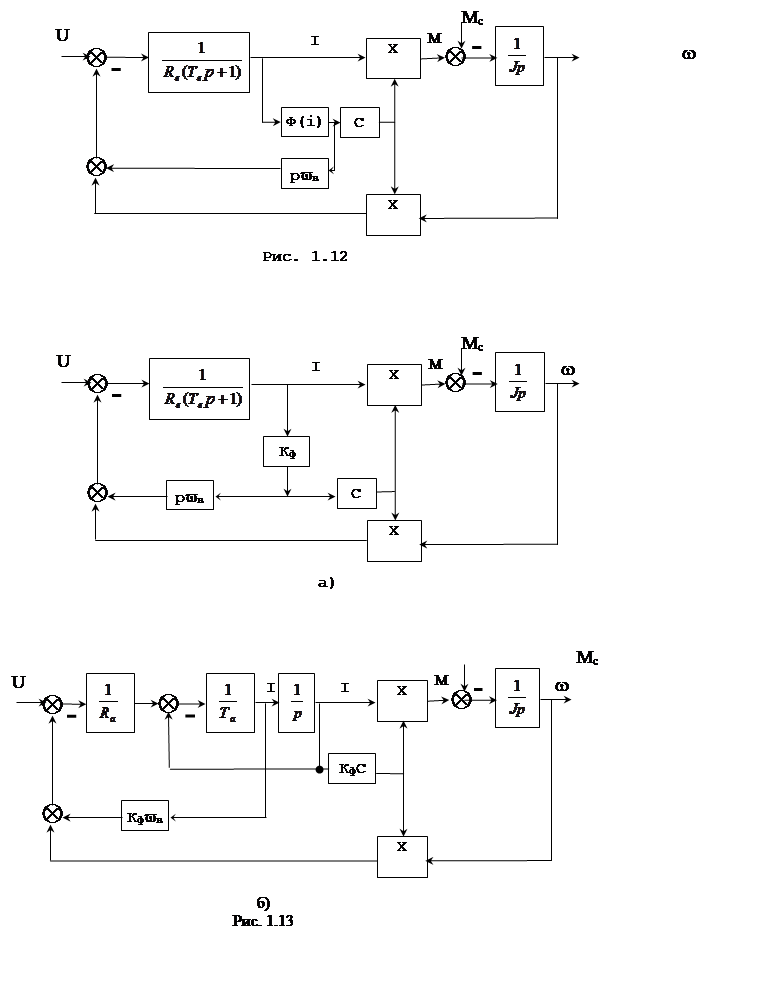1.7  Структурная схема двигателя со смешанным возбуждением.

Магнитный поток машины со смешанным возбуждением определяется суммарной намагничивающей силой, создаваемой обмотками независимого и смешанного возбуждения, т.е.

Где v_нв, v_пв – соответственно числа витков обмоток независимого и последовательного возбуждения; i_в, i – токи в обмотках независимого и последовательного возбуждения. Следовательно, используя результаты, полученные в п.п. 1.4, 1.7, структурную схему двигателя можно представить в виде на рис. 1.14. Линеаризованная модель показана на рис. 1.15. Здесь параметр К_ф есть коэффициент линеаризации нелинейной зависимости