Электрические двигатели в регулируемых электроприводах. Двигатели постоянного тока. Ограничения, накладываемые на режимы преобразования энергии в машинах постоянного тока, страница 12

2.11  Модель двигателя в установившихся режимах.

Полагая, что двигатель не получает электрическую энергию со стороны ротора и учитывая, что в установившемся режиме работы двигателя потокосцепление не изменяется, уравнения (8), (14) упрощаются:

,

Учитывая, что

,

, и отбрасывая индекс «w₁», получим:

,                     (2.40)

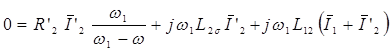.              (2.41)

Здесь w₁L_1s=х₁ – индуктивное сопротивление рассеяния статорной цепи, w₁L_2s=х’₂ – индуктивное сопротивление рассеяния вторичной цепи, w₁L₁₂-х_м – индуктивное сопротивление главного контура намагничивания, (w₁-w)/w=s – скольжение.

На основе уравнений (2.40), (2.41) можно составить схему замещения асинхронной машины, действительную для установившихся режимов (рис. 2.7).

 

2.12  Частотное регулирование скорости.

Выражения (2.30), (2.31) можно представить в виде:

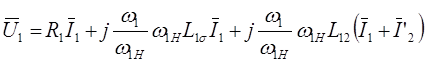,            (2.42)

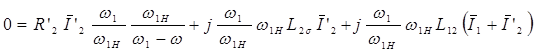.       (2.43) 

Здесь w_1н – угловая скорость вращения магнитного поля при номинальной частоте f_1н, w₁ – скорость вращения поля при произвольной частоте f₁.

В (2.43)величину (w₁-w)/w_1н=b принято называть абсолютным скольжением s=(w₁-w)/w₁ абсолютное скольжение связано соотношением s=b/a, где a=f₁/f_1н – относительная частота напряжения.

Будем полагать, что параметры схемы замещения фазы двигателя (рис. 2.7) определены при номинальной частоте, т.е. Тогда с учетом того, что w₁/w_1н=f₁/f_1н=a, уравнениям (2.42), (2.43) соответствует схема замещения, представленная на рис. 2.8.

 

Регулирование скорости двигателя может быть однозонным и двухзонным.

При однозонном регулировании (w₁ £ w_1н) по мере снижения частоты уменьшаются индуктивные параметры схемы замещения. Поэтому с целью исключения чрезмерного увеличения токов и следующего за этим повышения степени насыщения машины и увеличения потерь энергии одновременно со снижением частоты необходимо снижать и уровень напряжения.

Исходя из условия поддержания постоянства перегрузочной способности двигателя, характеризуемой отношением М_кр/М_с, где М_кр – критический момент, развиваемый двигателем, М_с – момент сопротивления на валу двигателя, М. П. Костенко был предложен закон частотного управления [10]

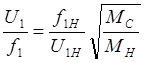,                        (2.34)

Где М_н – номинальный момент двигателя при f₁=f_1н.

Учитывая функциональные зависимости момента сопротивления от угловой скорости вращения, присущие произвольным механизмам, на основании (2.44) можно получить различные частные законы частотного управления:

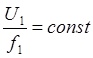  при М_С=const,                 (2.45)

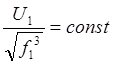 при М_С=,            (2.46)

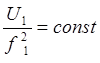  при М_С,                (2.47)

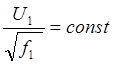  при М_С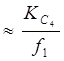.                (2.48)

В [8] показано, что в большинстве случаев можно ограничиться законом регулирования (2.45).

При условии U₁/f₁=const по мере снижения частоты возрастает доля напряжения в сопротивлении статора с ростом нагрузки, что приводит к уменьшению магнитного потока, и как следствие, к снижению электромагнитного момента (рис. 2.9).

С целью поддержания критического момента с уменьшением частоты используется компенсация падения напряжения в активном сопротивлении статора (I₁R₁ - компенсация) за счет введения положительных обратных связей по токам фаз статора. Такое управление в [8] названо скалярным частотным управлением с I₁R₁ – компенсацией.

 

Введение положительной обратной связи по вектору  приводит к увеличению критического момента при снижении частоты и повышению жесткости механических характеристик.

Для упрощенного формирования сигналов обратной связи быть использован модуль действующего значения тока статора или его активная составляющая, а так же (при использовании преобразователя частоты со звеном постоянного тока) ток в звене постоянного тока.