Электрические двигатели в регулируемых электроприводах. Двигатели постоянного тока. Ограничения, накладываемые на режимы преобразования энергии в машинах постоянного тока, страница 8

Допущение о неизменности индуктивного сопротивления цепи намагничивания основано на том, что в системах частотноуправляемого асинхронного электропривода потокосцепление поддерживается на заданном уровне. При этом обеспечивается неизменная степень насыщения магнитной системы, что предопределяет постоянство индуктивности. Постоянство индуктивных сопротивлений рассеяния объясняется тем, что в замкнутых системах элетропривода поддерживается низкое значение скольжения, вследствие чего явление вытеснения тока проявляется слабо.

Математическая модель двигателя строится также в предположении, что напряжения и токи нулевой последовательности отсутствуют, т.е. U_А+U_В+U_С=0, i_A+i_B+i_C=0.

2.4  Результирующие векторы напряжений, токов и потокосцеплений.

В симметричной машине с идеальными обмотками при питании ее симметричной системой напряжений и угловой частотой w, возникают симметричные системы токов статора и ротора и создаются симметричные системы той же частоты.

Фазные напряжения, токи и потокосцепления можно представить в виде соответствующих результирующих векторов. Результирующие векторы определяются таким образом, чтобы их проекции на оси обмоток А, В, С в любой момент времени соответствовали мгновенным фазным значениям соответствующих величин. В [4] показано, что если известны мгновенные значения Х_А, Х_В, Х_С некоторой координаты, то результирующий вектор Х определяется следующим выражением:

Здесь

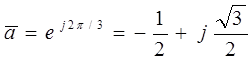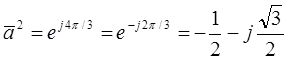Направление оси обмотки фазы А статора принимается за положительное направление вещественной оси в неподвижной системе координат с осями ab.

Так как мгновенные значения Х_А, Х_В, Х_С представляют собой вещественные числа, то численные значения Х_А, Х_В, Х_С откладываются на вещественной оси a.

Порядок построения результирующего вектора:

1. На вещественной оси a отложить числовые значения Х_А, Х_В, Х_С;

2. Вектор Х_В повернуть на угол 2p/3 в положительном направлении;

3. Вектор Х_С повернуть на угол 4p/3 в положительном направлении или на -2p/3 в отрицательном направлении;

4. Сложить векторы Х_А, аХ_В, а²Х_С и определить 2/3 этой суммы.

jb

jb

В качестве примера на рис. 2.1 приведена последовательность операций по определению результирующего вектора Х при Х_А=9, Х_В=-3, Х_С=-6.

 

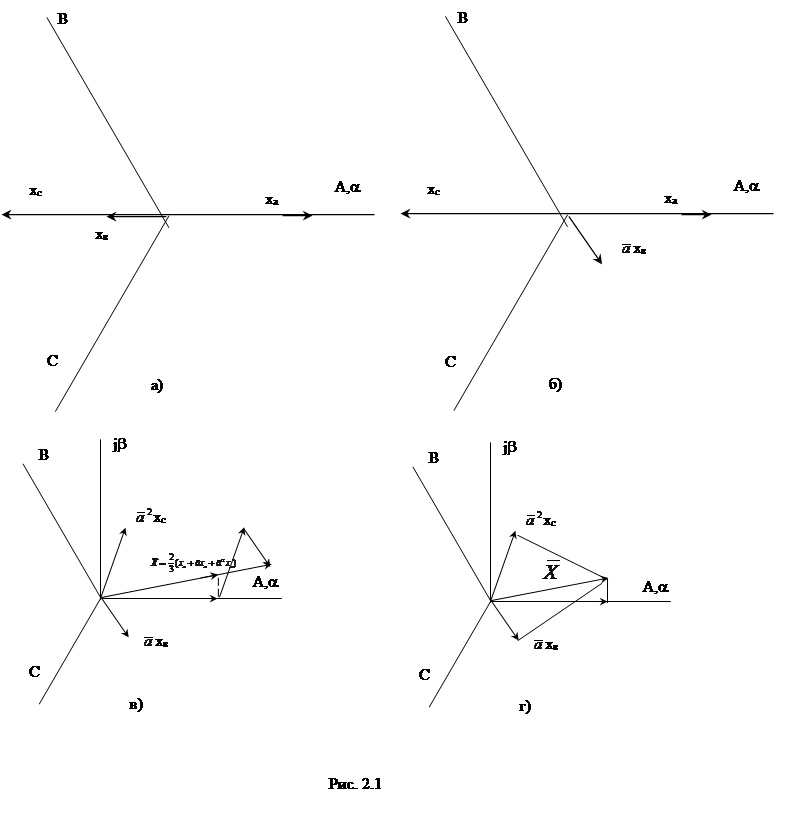Из построения следует, что проекции вектора Х на оси обмоток фаз А, В, С дают как величину, так и знак мгновенных значений Х_А, Х_В, Х_С.

Результирующий вектор Х можно разложить по ортогональным осям a,b. Так как то с учетом условия Х_А+Х_В+Х_С=0 получим:

(2.1)

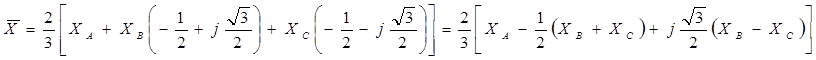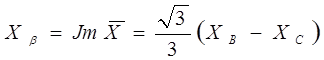Таким образом, с помощью формул (2.1) для каждлго момента времени можно определить значения напряжений, токов или потокосцеплений в ортогональной системе координат a,b по значениям соответствующих переменных в системе координат А, В, С, т.е. преобразование 3®2.

При построении систем управления электроприводами возникает необходимость обратного преобразования.

Проекция Х_А определяется непосредственно из первого выражения системы (1).

Так как X_С =-(Х_А+Х_В),то

Аналогичным образом получим:

Таким образом, преобразование 2®3 осуществляется с использованием формул:

Х_А = Х_a,                                                  (2.2)  

2.5  Представление результирующего вектора в различных системах координат.

Результирующий вектор Х можно рассматривать не только в неподвижной системе координат a,b, но и в ортогональных системах координат, вращающихся с некоторой скоростью w_к (система координат a,b является частным случаем при w_к=0). Распространенными являются следующие варианты: