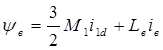
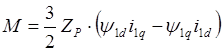
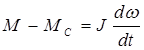
Соответствующая структурная схема представлена на рис. 3.3.
3.12 Структурная схема двигателя с постоянными магнитами.
При рассмотрении электромеханических процессов потокосцепление, создаваемое постоянными магнитами, можно считать неизменным: yв=const. Взаимодействие обмоток фаз статора и пусковой (демпферной) обмотки с постоянными магнитами можно приближенно учесть введением соответствующих составляющих в выражения, описывающие формирование потокосцеплений фаз статора и пусковой (демпферной) обмотки. Тогда система уравнений (3.10) преобразуется к виду:
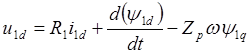
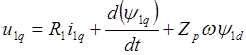
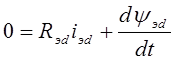
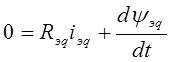
(3.13)
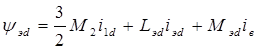
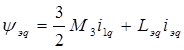
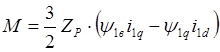
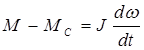
Подставив в первые четыре выражения
для потокосцеплений и учитывая, что dyв/dt=0,
получим систему уравнений:
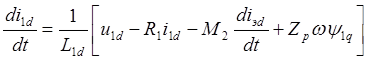
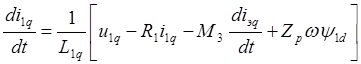
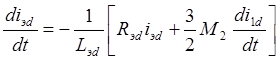(3.14)
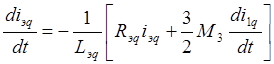
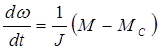
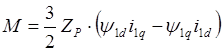
Соответствующая системе уравнений (3.14) структурная схема приведена на рис.3.4. в большинстве случаев можно принять: k1=0.
3.13 Модель двигателя в установившихся режимах.
При работе в двигательном режиме ротор отстает от магнитного поля статора на угол q=w1t-ZPwt, который принято называть углом нагрузки или рабочим углом.
В установившихся режимах пусковая (демпферная) обмотка в формировании электромагнитного момента не участвует.
Принимая dy1d/dt=0, dy1q/dt=0, уравнения, описывающие
протекающие в двигателе процессы, запишем в следующем виде:
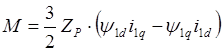(3.15)
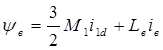
Для двигателя с постоянными магнитами в формуле для вычисления y1d слагаемое M1iв следует заменить на к1yв, а последнее уравнение исключить.
Если обмотки фаз статора эквивалентной двухфазной синхронной машины питаются симметричной двухфазной системой напряжений
То 
,
.
Подставив y1d, y1q в первое, второе и четвертое уравнения и пренебрегая активным сопротивлением обмотки статора, как обычно поступают при анализе установившихся режимов двигателей мощностью свыше 10 кВт [3,5], запишем:
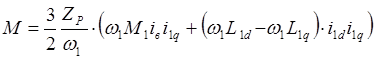
Введем обозначения: w1L1q=x1q, w1L1d=x1d. Учтем, что w1M1iв представляют собой амплитуду противоЭДС. Тогда:
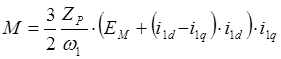
Следовательно,
, 
,
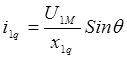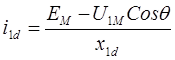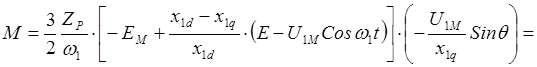
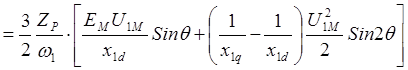
Переходя от амплитудных значений напряжения U1M и противоЭДС EM к эффективным (действующим) значениям U1 и Е и учитывая, что w/Zp=w0, где w0 –скорость идеального холостого хода двигателя окончательно получаем:
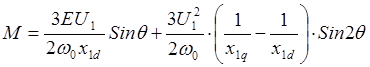(3.16)
Из
(3.16) следует, что явнополюсное исполнение ротора вызывает появление
(рис.3.5), кроме основной составляющей M1=M1MSinq,
M1M=3U1E/w0x1d, еще и реактивной составляющей M2=M2MSin2q,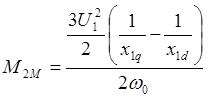 
электромагнитного
момента. Максимуму момента соответствует угол qМ, который можно определить из условия
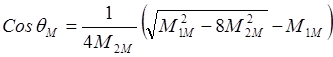. Реактивный момент M2
при ½q½<qМ вызывает некоторый рост
электромагнитного момента (рис.3.4). Двигатель может работать в установившемся
режиме, если -qМ<q<qМ. Номинальному режиму соответствует рабочий
угол qН=p/9…p/6.
При отклонении от рабочего угла q от значения q0, с которым двигатель работал в установившемся режиме, возникает синхронизирующий момент, под воздействием которого устойчивое состояние работы восстанавливается. Если отклонение Dq=q-q0 незначительно, то синхронизирующий момент
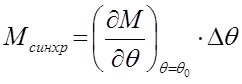(3.17)
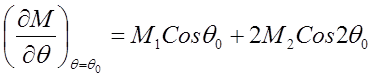
Режим работы синхронной машины устойчив, если Мсинхр>0.
В приближенном выражении (3.7) не учтен асинхронный момент, возникающий при w¹w1. создаваемый пусковой (демпферной) обмоткой асинхронный момент можно считать пропорциональным скольжению. Учитывая, что асинхронный момент можно оценить выражением
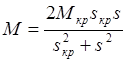(3.18)
И вычисляя производную, находим:
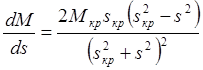
Перейдем к конечным приращениям и определим отклонение DМ/Ds при начальном скольжении sнач=0. Так как Ds=sнач-s=-s=-Dw/w1, то жесткость механической характеристики, создаваемой пусковой (демпферной) обмоткой определим следующим образом:
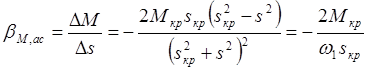(3.19)
Следовательно, формирование синхронизирующего момента можно представить в виде структурной схемы, приведенной на рис.3.6.
Обычно принимают:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.