Моделирование случайных величин. Методы генерирования на ЭВМ случайных величин с различными законами распределения, страница 9

Так как на начальном участке при малых значениях произведения a генерируемые числа возрастают (см. п. 3 раздела 1.1), то можно считать, что он распространяется до первого максимума.

Другой, более точный способ нахождения начального участка сводится к определению периода повторения чисел с использованием метода подвижного окна.

Сначала фиксируем три первых числа и с помощью окна из трех чисел пытаемся найти такие же три числа в сгенерированной последовательности чисел. Если повторяющихся групп из трех чисел нет, то берем новые три числа со сдвигом на одно число и снова пытаемся найти такие же три числа. Если попытка снова неуспешна, то сдвигаем начальные числа на одно число и т. д., пока не найдем повторяющуюся тройку чисел. Так определим период повторения чисел и начальный участок (до первой тройки чисел, для которой нашлась другая такая же тройка чисел).

ЗАМЕЧАНИЕ: Участок с последовательно возрастающими числами может появиться там, где очередное произведение a окажется малым. Для исключения таких участков следует брать каждое очередное число через n_нач чисел.

3.3. ОЦЕНКА КАЧЕСТВА ГЕНЕРИРУЕМОЙ ПОСЛЕДОВАТЕЛЬНОСТИ ПО БЛИЗОСТИ ХАРАКТЕРИСТИК ЕЕ РАСПРЕДЕЛЕНИЯ К ТЕОРЕТИЧЕСКИМ ЗНАЧЕНИЯМ

Пусть теоретические значения математического ожидания и дисперсии случайной величины ξ, подчиняющейся некоторому закону распределения, равны M_ξ, и D_ξ.

Экспериментальные оценки этих характеристик получаются по формулам

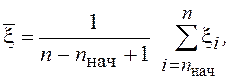
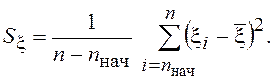
При вычислениях на ЭВМ дисперсию удобно вычислять по формуле

.

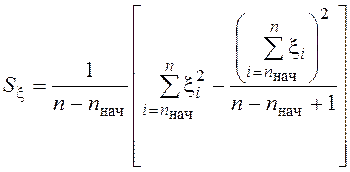Близость оценки математического ожидания и его теоретического значения оценивается по критерию Стьюдента выражением

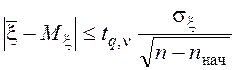                    ,                                        (18)

где  – оценка среднеквадратического отклонения случайной величины .

Если неравенство (18) не выполняется, то отклонение значимо и распределение нельзя считать соответствующим теоретическому.

Значение определяется по табл. 2 или табл. 3, но .

Близость дисперсий по критерию Фишера оценивается выражением

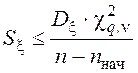,                                                        (19)

где  – коэффициент, определяемый по таблице –распределения для q=0.01, 0.05, 0.1 и  степеней свободы (см. табл. 4).

Таблица 4

Значения верхнего предела  в функции q и ν

ν	q			ν	q			ν	q
	0.10	0.05	0.01		0.10	0.05	0.01		0.10	0.05	0.01
1	2.7	3.8	6.6	11	17.3	19.7	24.7	21	29.6	32.7	38.9
2	4.6	6.0	9.2	12	18.5	21.0	26.2	22	30.8	33.9	40.3
3	6.3	7.8	11.3	13	19.8	22.4	27.7	23	32.0	35.2	41.6
4	7.8	9.5	13.3	14	21.1	23.7	29.1	24	33.2	36.4	43.0
5	9.2	11.1	15.1	15	22.3	25.0	30.6	25	34.4	37.7	44.3
6	10.6	12.6	16.8	16	23.5	26.3	32.0	26	35.6	38.9	45.6
7	12.0	14.1	18.5	17	24.8	27.6	33.4	27	36.7	40.1	47.0
8	13.4	15.5	20.1	18	26.0	28.9	34.8	28	37.9	41.3	48.3
9	14.7	16.9	21.7	19	27.2	30.1	36.2	29	39.1	42.6	49.6
10	16.0	18.3	23.2	20	28.4	31.4	37.6	30	40.3	43.8	50.9