Моделирование случайных величин. Методы генерирования на ЭВМ случайных величин с различными законами распределения, страница 3

В силу конечности М и рекуррентности алгоритма через некоторое время числа начнут повторяться.

При больших М и малых a период оказывается достаточно большим, например, при a = 23 и М = 10⁸ период 5 882 352 числа. В общем случае, период тем больше, чем больше М и меньше a. М определяет период повторения чисел, а a – степень случайности.

4.  Если a много меньше М, а  малое, то в начале последовательности или там, где получилось малое очередное значение , наблюдается неслучайный участок с последовательно возрастающими по закону  числами, которые нельзя рассматривать случайными. Поэтому a должно быть достаточно большим, что противоречит требованию п. 3. Чтобы уменьшить длину этого участка,  следует брать примерно равным M/(5a).

Из–за этих причин получаемое распределение называют квазиравномерным, а числа последовательности – псевдослучайными.

При работе с целыми числами для обеспечения условий 1 – 4 принимают:

a – простое (нечетное) число (3, 5, 7, 11, 13, 17, 19, 23 и т.д.);

 – любое достаточно большое число;

М – четное не кратное a и достаточно большое число;

b – любое число, близкое .

Функция плотности вероятностей равномерного распределения на интервале (a, b) имеет вид

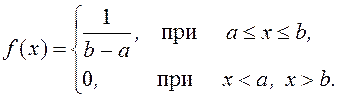
Математическое ожидание и дисперсия случайной величины x здесь равны

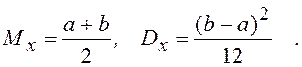
Для получения последовательности случайных чисел x_i, равномерно распределенных на интервале (a, b), следует воспользоваться формулой

, где  – значение случайной величины, равномерно распределенной на интервале (0, 1).

1.2. ЭКСПОНЕНЦИАЛЬНОЕ РАСПРЕДЕЛЕНИЕ

Плотность распределения вероятностей этого закона имеет вид

Математическое ожидание и дисперсия здесь равны

Для получения случайных величин x_i, имеющих экспоненциальное распределение, воспользуемся непосредственным решением уравнения (1), в котором нижний предел интегрирования заменен на 0, так как этот закон справедлив только при х>0

.

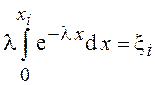После интегрирования получим

.

Решая это уравнение относительно x_i и, учитывая, что распределения  и  эквивалентны, будем иметь

.

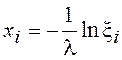Алгоритм моделирования экспоненциального распределения сводится к вычислениям согласно данной формулы.

1.3. ДВУХПАРАМЕТРИЧЕСКОЕ ЭКСПОНЕНЦИАЛЬНОЕ РАСПРЕДЕЛЕНИЕ

При решении практических задач часто приходится оперировать со случайными величинами, минимальное значение которых ограничено некоторой постоянной величиной x=b. Такие величины применяются, например, для описания времени восстановления аппаратуры. Физически это означает, что во всех случаях для устранения неисправности требуется некоторое время .

Плотность вероятности этого распределения имеет вид (так называемая сдвинутая экспонента)

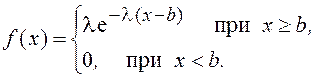
Математическое ожидание и дисперсия здесь равны

Рассмотрим, как получить на ЭВМ последовательность значений случайной величины с таким распределением.

Используем функциональное уравнение

.

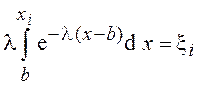После обычных преобразований получим рабочую формулу

.

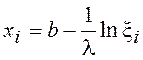Второе слагаемое в правой части формулы представляет собой случайную величину, подчиненную экспоненциальному распределению с параметром . Следовательно, формирование случайной величины со сдвинутым экспоненциальным распределением сводится к получению (любым способом) экспоненциально распределенной случайной величины и суммированию ее с константой b.

1.4. НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ

Воспользуемся центральной предельной теоремой Ляпунова из теории вероятностей. В простейшей форме сущность этой теоремы состоит в том, что

закон распределения суммы m независимых случайных величин, имеющих один и тот же произвольный закон распределения, при неограниченном увеличении числа слагаемых m приближается к нормальному.

В случае равномерно распределенных в интервале (a, b) независимых случайных чисел сумма m таких чисел стремится к нормальному распределению с математическим ожиданием

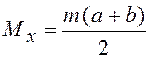
и дисперсией