Моделирование случайных величин. Методы генерирования на ЭВМ случайных величин с различными законами распределения, страница 11

Программа должна содержать подпрограммы определения математического ожидания, дисперсии, величины  и нормированной автокорреляционной функции.

Проанализировать полученные значения автокорреляционной функции, определить n_нач. и скорректировать программу так, чтобы исключить влияние n_нач .

Произвести проверку гипотезы о равномерности распределения.

Пример окна программы п. 2, составленной в DELPHI, показан на рис.3.

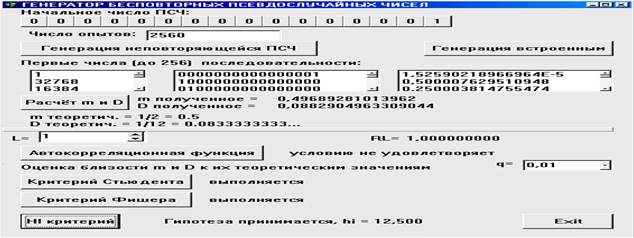Рис. 3

3.  Составить программу генерирования случайных чисел с заданным законом распределения. Программа должна содержать подпрограммы определения математического ожидания, дисперсии, величины  и нормированной автокорреляционной функции.

Произвести проверку соответствия полученного закона распределения случайных чисел заданному.

5. КОНТРОЛЬНЫЕ ВОПРОСЫ

1.  В чем заключается сущность теоремы, на которой базируется моделирование случайных чисел на ЭВМ?

2.  Какие методы моделирования на ЭВМ случайных чисел с различными законами распределения вы знаете?

3.  Приведите рекуррентные формулы генерирования случайных чисел с равномерным законом распределения на интервале (0, 1).

4.  Приведите формулу моделирования равномерного распределения на интервале (a, b).

5.  Приведите формулу моделирования экспоненциального распределения.

6.  Приведите формулу моделирования нормального распределения с параметрами M_x= 0, D_x= 1.

7.  Приведите формулу моделирования распределения Эрланга.

8.  Приведите формулу моделирования распределения .

9.  Как определяется вероятность k–ого события?

10. Как определяется k–е событие, если его вероятность задана?

11. Почему можно применить односторонний предел в формуле (15)?

12. Приведите формулу распределения Пуассона.

13. В чем различие распределений Паскаля и биномиального?

14. Как генерируются бесповторные случайные числа?

15. Как проверить наличие начального неслучайного участка в программе генерирования случайных чисел? Как избавиться от его влияния?

16. Как определить период последовательности генерируемых чисел?

17.  Какие критерии оценки близости распределения Вы знаете?

18.  Приведите условия принятия гипотезы об эквивалентности математических ожиданий.

19.  Приведите условия принятия гипотезы об эквивалентности дисперсий.

20.  В чем заключается сущность критерия ?

СПИСОК ЛИТЕРАТУРЫ

1.  Ермаков С.М., Михайлов Г.А. Статистическое моделирование. М.: Наука, 1982. – 296 с.

2.  Айвазян С.А., Мешалкин Л.Д., Енюков И.С. Прикладная статистика: Основы моделирования и первичной обработки данных. М.: Финансы и статистика, 1985. – 470 с.

3.  Давидович М.И., Петрович М.Л. Статистическое оценивание и проверка гипотез.  М.: Финансы и статистика, 1989. – 191 с.

4.  Гилл А. Линейные последовательностные машины. М.: Наука, 1974. –288 с.

5.  Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. М.: Наука, 1970. – 720 с.

Учебное издание

Дорошенко Александр Николаевич,

Федоров Валентин Николаевич

МОДЕЛИРОВАНИЕ СЛУЧАЙНЫХ ВЕЛИЧИН

Учебное пособие

–––––––––––––––––––––––––––––––––––––––––––––––––––––––––––

Подписано в печать 13.11.2003 г.

Формат 60х84  1/16

Объем 2.0 п.л.      Тираж 100 экз.     Заказ 195

–––––––––––––––––––––––––––––––––––––––––––––––––––––––––––

Отпечатано в типографии Московской государственной академии

 приборостроения и информатики

107846, Москва, ул. Стромынка, 20