При ![]()
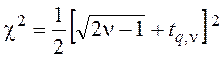 , где
, где ![]() берется из табл. 3.
берется из табл. 3.
Если неравенство (19) не выполняется, то распределение нельзя считать соответствующим теоретическому.
Такая оценка проводится с помощью критерия ![]() , сущность которого для нашего случая сводится к следующему. (Символ
, сущность которого для нашего случая сводится к следующему. (Символ ![]() – это условное обозначение распределения, а не квадрат переменной χ).
– это условное обозначение распределения, а не квадрат переменной χ).
Сгенерируем n
чисел. Разобьем диапазон значений полученных чисел на k не обязательно равных интервалов так, чтобы в каждом из них содержалось
не менее 5 чисел. (Оптимальное значение k
определяется из выражения ![]() .) Для каждого интервала определим количество реально попавших в него
чисел ni и количество чисел, могущих в него попасть теоретически npi, где pi - теоретическая
вероятность попадания числа в i–й интервал.
.) Для каждого интервала определим количество реально попавших в него
чисел ni и количество чисел, могущих в него попасть теоретически npi, где pi - теоретическая
вероятность попадания числа в i–й интервал.
Вычислим величину
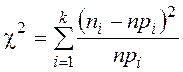 , (20)
, (20)
представляющую собой взвешенную сумму квадратов отклонений реальных и теоретических значений вероятностей попадания числа в i–й интервал.
Случайная величина ![]() обладает
тем свойством, что ее распределение не зависит от распределения исследуемых
чисел, а только от количества интервалов k, а
точнее, от параметра
обладает
тем свойством, что ее распределение не зависит от распределения исследуемых
чисел, а только от количества интервалов k, а
точнее, от параметра ![]() –
числа степеней свободы, определяемого здесь как
–
числа степеней свободы, определяемого здесь как ![]() , где s – число используемых ограничений, например таких
, где s – число используемых ограничений, например таких
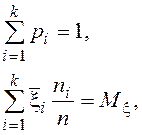
где ![]() – среднее значение случайной величины на i–ом интервале,
– среднее значение случайной величины на i–ом интервале,
 .
.
В нашем случае ![]() и
и ![]() известны (мы генерируем случайные величины с заданными значениями mξ и Dξ), поэтому число
степеней свободы
известны (мы генерируем случайные величины с заданными значениями mξ и Dξ), поэтому число
степеней свободы ![]() .
.
Для распределения ![]() имеются
таблицы (см. табл. 4), по которым, зная конкретное значение
имеются
таблицы (см. табл. 4), по которым, зная конкретное значение ![]() и
и ![]() ,
можно найти вероятность q того, что величина,
распределенная по закону
,
можно найти вероятность q того, что величина,
распределенная по закону ![]() ,
превзойдет это значение.
,
превзойдет это значение.
Проверку гипотезы о совпадении полученного распределения с теоретическим производят следующим образом.
Задавшись вероятностью q (0.01, 0.05, 0.1), по ![]() находят
в таблице
находят
в таблице ![]() –распределения
значение
–распределения
значение ![]() . Если
определенное по формуле (20) значение
. Если
определенное по формуле (20) значение ![]() не
превосходит
не
превосходит ![]() , то
гипотеза о совпадении полученного и теоретического распределения принимается.
Если
, то
гипотеза о совпадении полученного и теоретического распределения принимается.
Если ![]() , то эта гипотеза отвергается.
, то эта гипотеза отвергается.
Следует отметить, что проверка гипотезы по
критерию ![]() сама
по себе не дает доказательства, правильна или ложна эта гипотеза. Она лишь указывает
степень согласия гипотезы с результатами эксперимента.
сама
по себе не дает доказательства, правильна или ложна эта гипотеза. Она лишь указывает
степень согласия гипотезы с результатами эксперимента.
Критерий проверки (вероятность q) выбирают таким, чтобы вероятность отвергнуть гипотезу, когда она верна, была малой. Поэтому q выбирают обычно равной одному из значений 0.01, 0.05, 0.1.
Замечание: Критерием ![]() можно пользоваться и без таблиц, если применить формулу Романовского
можно пользоваться и без таблиц, если применить формулу Романовского
![]()
Если
![]() , то согласие между
эмпирическим и теоретическим распределениями можно считать удовлетворительным.
, то согласие между
эмпирическим и теоретическим распределениями можно считать удовлетворительным.
1. Составить программу генерирования случайных чисел с равномерным
распределением на интервале (0, 1), обеспечив возможность варьирования
параметров ![]() , a, b, M.
, a, b, M.
Программа должна
содержать подпрограммы определения математического ожидания, дисперсии,
величины ![]() и
нормированной автокорреляционной функции.
и
нормированной автокорреляционной функции.
Проанализировать полученные значения автокорреляционной функции, определить nнач. и скорректировать подпрограммы так, чтобы исключить nнач .
Произвести проверку гипотезы о равномерности распределения.
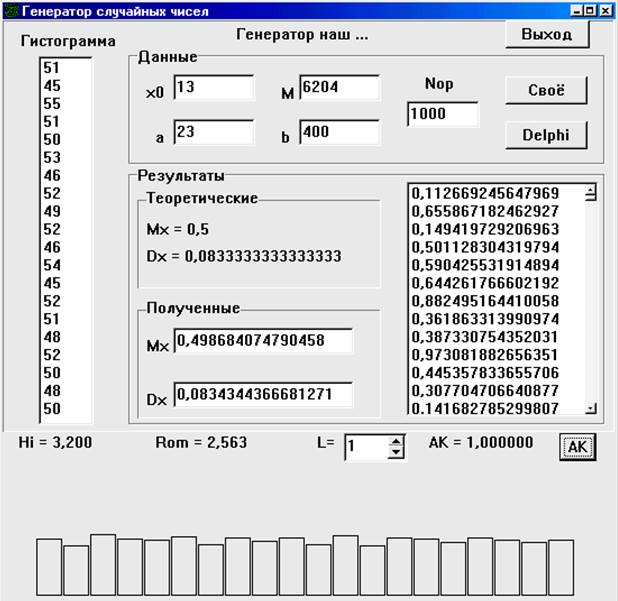
Пример окна программы п. 1, составленной в DELPHI, показан на рис.2.
 |
2. Составить программу генерирования бесповторных случайных чисел для n = 16, обеспечив возможность варьирования начального значения X0 .
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.