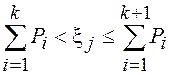Моделирование случайных величин. Методы генерирования на ЭВМ случайных величин с различными законами распределения, страница 6

.                                                  (15)

Для фиксированного  неравенство выполняется лишь при одном значении k. Это значение k и определяет номер события A_k , которое произошло в данном опыте. Cвершение события A_k означает, что случайная величина x приняла значение k.

В рассматриваемых ниже законах суммы вероятностей монотонно возрастают с ростом i, поэтому вместо неравенства (15) можно использовать одностороннюю границу вида

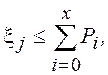                                                    (16)

а поиск значения x производить последовательным вычитанием P_i  из  до первого результата, не превышающего 0. Значение i, при котором это произойдет, и принимается за значение случайной величины x.

Вычисления реализуются достаточно просто, так как для рассматриваемых законов очередное значение вероятности P_i+1 определяется по рекуррентной формуле вида

P_i+1 = P_i r(i) ,

где r(i) – определяется законом распределения случайной величины.

2.1. Распределение Пуассона

Это распределение описывает поведение редких событий и широко применяется в теории массового обслуживания, в теории надежности и ряде других областей науки и техники. Оно задается рядом распределения

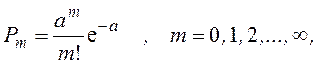
где  – вероятность того, что случайная величина x примет значение m .

Для этого распределения справедливо

что используется обычно для предварительной проверки того, что случайная величина x подчиняется закону Пуассона.

Для этого закона неравенство (16) имеет вид

где

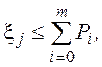
2.2. Геометрическое распределение

Это распределение задает вероятность того, что некоторое событие A произойдет в первый раз после точно k опытов, если вероятность появления события в одном опыте равна p,

где k – целое число,

Математическое ожидание и дисперсия этого распределения равны

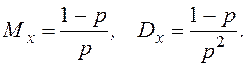
Неравенство (16) здесь имеет вид

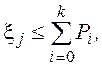
где

Для этого закона можно получить и другое выражение, удобное для вычислений. Действительно, для интегрального закона этого распределения имеем

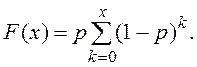
Воспользовавшись формулой суммы x членов геометрической прогрессии со знаменателем 1 – p, получим

Поэтому для определения x здесь можно применить неравенство

Решение находится последовательным увеличением x до тех пор, пока правая часть неравенства станет не меньше .

2.3. ГИПЕРГЕОМЕТРИЧЕСКОЕ РАСПРЕДЕЛЕНИЕ

При этом распределении вероятность того, что случайная бесповторная выборка объемом n содержит точно x элементов типа A, если эта выборка производится из генеральной совокупности из N элементов, среди которых M = pN элементов принадлежат типу A, равна

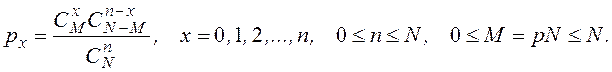
Математическое ожидание и дисперсия этого распределения равны

Здесь p доля элементов типа A в генеральной совокупности N.

При моделировании такого распределения используется выражение

2.4. распределение Паскаля

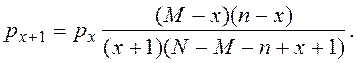
Это распределение задается рядом

 

Вероятность  есть вероятность появления события в m–й раз после точно m+x–1 опытов при вероятности появления события в одном опыте равной p.

При m =1 распределение Паскаля сводится к геометрическому.

Математическое ожидание и дисперсия для этого распределения равны

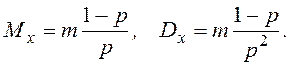
          Значение x при заданном m определяется решением неравенства (16), где

2.5. Биномиальное распределение

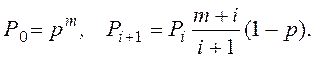
Для этого распределения вероятность того, что в серии из n опытов событие A, имеющее вероятность появления в одном опыте p, произойдет ровно x раз, задается рядом

Математическое ожидание и дисперсия этого распределения равны

Моделирование этого распределения сводится к получению последовательности целочисленных значений x при заданных p и n, которые определяются решением неравенства (16), где

2.6. БЕСПОВТОРНЫЕ СЛУЧАЙНЫЕ ЧИСЛА

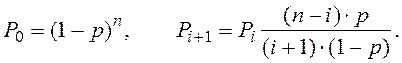
В случае, когда необходимы бесповторные случайные числа, можно воспользоваться принципами создания автономной линейной последовательностной машины (АЛПМ) или покоящейся линейной последовательностной машины (ПЛПМ), которые способны генерировать 2ⁿ–1 различных двоичных чисел, где n – разрядность машины.