Моделирование случайных величин. Методы генерирования на ЭВМ случайных величин с различными законами распределения, страница 2

Для использования этой формулы необходимо располагать n значениями а_k, которые рассчитываются для заданного закона распределения f(x) и вводятся в оперативную память ЭВМ в порядке возрастания. Простейшая процедура расчета величин а_k основана на предположении, что вероятность попадания в любой из n интервалов одинакова и равна, очевидно, 1/n. Это означает, что мы выбираем такие интервалы, в которых приращение функции распределения F(x) при переходе от k–го к (k+1)–му интервалу было постоянным и равным 1/n, т.е.

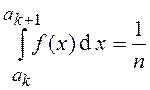.                                            (3)

Вследствие нелинейности функции распределения F(x) (за исключением равномерного распределения) длина интервалов (а_k, а_k+1) получается различной.

Начальное значение а_k =а₀ всегда известно – оно равно минимальному значению случайной величины х. Следовательно, соотношение (3) позволяет последовательно вычислить все а_k (k = 1, …, n), т.е. решается оно относительно верхнего предела интегрирования. Значение n обычно принимается равным 2^m, где m=4…6 (n=16…64).

Для организации случайной выборки k–го интервала из равномерного распределения извлекается случайное целое число  и первые m разрядов используются в качестве адреса для выбора из таблицы значений а_k и а_{k +1}. Затем по формуле (2) определяется значение х_i, при этом используется уже новое случайное число .

Данный метод формирования случайных чисел находит широкое практическое применение благодаря своей универсальности и экономичности. Его недостатком является неравномерная точность аппроксимации.

Из рассмотрения методов моделирования случайных величин следует, что для их реализации необходимо иметь случайную величину ξ с равномерным распределением либо на интервале (0,1), либо на интервале (а_k,а_{k +1}), в общем случае на интервале (a, b).

1.1. МОДЕЛИРОВАНИЕ РАВНОМЕРНОГО РАСПРЕДЕЛЕНИЯ

Случайная величина , равномерно распределенная на интервале (0,1), имеет плотность распределения

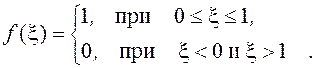
Ее математическое ожидание и дисперсия равны

У ряда ЭВМ имеются специальные датчики случайных равномерно распределенных чисел, использующие либо физические принципы получения случайных чисел (например, шумы в электронных приборах, радиоактивный распад и т.п.), либо микропрограмму.

Датчики случайных равномерно распределенных на интервале (0, 1) чисел имеются также во всех языках программирования высокого уровня (процедуры RANDOM).

В случае, когда таких датчиков нет, можно получить случайные числа программным способом. Наиболее часто для этого используют одно из рекуррентных соотношений:

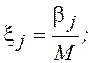
                         ,      j =0,1,2,…             (4)

где операция mod M означает остаток от деления  на М; a и М – константы (положительные числа);

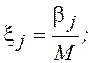
                         ,                           (5)

где b – положительное число.

Выбирая , a, b и М, необходимо учитывать следующее:

1.  Произведение  в формуле (4) не должно быть кратным М. Иначе можно получить последовательность нулей. Для формулы (5) получение 0 не опасно. Поэтому для (4) , а для (5) .

2.  Произведение  в (4) или выражение  в (5) не должны превышать максимально возможное для ЭВМ число, т.е.

;         .

В соответствии с алгоритмом получения случайных чисел

, поэтому должно быть

,   

, откуда

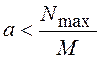         для (4)

и                                

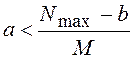    для (5).

3.  Полученные таким способом числа, строго говоря, не являются случайными, т.к. рекуррентный способ образования последовательности позволяет по известному числу этой последовательности (например, первому) однозначно определить все остальные. При этом не исключена возможность образования периодически повторяющихся циклов. Это объясняется тем, что при значениях

 ведет себя как показательная функция , которая при достижении значения М скачком изменяется до нового начального значения  и снова растет как  до М.