Моделирование случайных величин. Методы генерирования на ЭВМ случайных величин с различными законами распределения

МИНИСТЕРСТВО ОБРАЗОВАНИЯ

РОССИЙСКОЙ ФЕДЕРАЦИИ

––––––––––––––

МОСКОВСКАЯ ГОСУДАРСТВЕННАЯ АКАДЕМИЯ ПРИБОРОСТРОЕНИЯ И ИНФОРМАТИКИ

––––––––––––––––––––––

Кафедра “Персональные компьютеры и сети”

_______________________________________________

,

МОДЕЛИРОВАНИЕ СЛУЧАЙНЫХ ВЕЛИЧИН

Учебное пособие

Москва

2003

УДК: 519.21(075.8)

Моделирование случайных величин/ А.Н. ,

– М.: МГАПИ, 2003.– 32 с.

ISBN 5-8068-2

Рекомендовано Ученым Советом МГАПИ в качестве учебного пособия для специальности 2201.

Рецензенты:  канд. техн. наук профессор

канд. техн. наук профессор

Рассмотрены методы генерирования на ЭВМ случайных величин с различными законами распределения и оценки качества полученных распределений. Может быть использовано при выполнении лабораторных и учебно-исследовательских работ, курсовых и дипломных проектов.

Предназначено для студентов специальности 22.03.

___________________

ISBN 5-8068-2

Ó ,

, 2003

СОДЕРЖАНИЕ

1. моделирование непрерывных распределений.. 4

1.1. МОДЕЛИРОВАНИЕ РАВНОМЕРНОГО РАСПРЕДЕЛЕНИЯ.. 5

1.2. ЭКСПОНЕНЦИАЛЬНОЕ РАСПРЕДЕЛЕНИЕ. 8

1.3. ДВУХПАРАМЕТРИЧЕСКОЕ ЭКСПОНЕНЦИАЛЬНОЕ РАСПРЕДЕЛЕНИЕ. 8

1.4. НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ. 9

1.5. ЛОГАРИФМИЧЕСКИ НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ. 10

1.6. гамма – распределение. 11

1.7. РАСПРЕДЕЛЕНИЕ ЭРЛАНГА.. 11

1.8. РАСПРЕДЕЛЕНИЕ хи–квадрат. 12

1.9. РАСПРЕДЕЛЕНИЕ СТЬЮДЕНТА.. 13

1.10. РАСПРЕДЕЛЕНИЕ ФИШЕРА.. 14

1.11. БЕТА–РАСПРЕДЕЛЕНИЕ. 14

1.12. РАСПРЕДЕЛЕНИЕ ВЕЙБУЛЛА.. 15

1.13. РАСПРЕДЕЛЕНИЕ РЕЛЕЯ.. 15

2. МОДЕЛИРОВАНИЕ ДИСКРЕТНЫХ РАСПРЕДЕЛЕНИЙ.. 17

2.1. Распределение Пуассона.. 17

2.2. Геометрическое распределение. 18

2.3. ГИПЕРГЕОМЕТРИЧЕСКОЕ РАСПРЕДЕЛЕНИЕ. 19

2.4. распределение Паскаля.. 19

2.5. Биномиальное распределение. 19

2.6. БЕСПОВТОРНЫЕ СЛУЧАЙНЫЕ ЧИСЛА.. 20

3. ОЦЕНКА КАЧЕСТВА ГЕНЕРИРУЕМОЙ ПОСЛЕДОВАТЕЛЬНОСТИ СЛУЧАЙНЫХ ЧИСЕЛ.. 22

3.1. КРИТЕРИИ ОЦЕНКИ КАЧЕСТВА.. 22

3.2. ОПРЕДЕЛЕНИЕ И АНАЛИЗ НОРМИРОВАННОЙ АВТОКОРРЕЛЯЦИОННОЙ ФУНКЦИИ.. 22

3.3. ОЦЕНКА КАЧЕСТВА ГЕНЕРИРУЕМОЙ ПОСЛЕДОВАТЕЛЬНОСТИ ПО БЛИЗОСТИ ХАРАКТЕРИСТИК ЕЕ РАСПРЕДЕЛЕНИЯ К ТЕОРЕТИЧЕСКИМ ЗНАЧЕНИЯМ... 24

3.4. ОЦЕНКА КАЧЕСТВА ГЕНЕРИРУЕМОЙ ПОСЛЕДОВАТЕЛЬНОСТИ ПО БЛИЗОСТИ ЕЕ РАСПРЕДЕЛЕНИЯ К ТЕОРЕТИЧЕСКОМУ.. 26

4. ЗАДАНИЕ для самостоятельной РАБОТЫ... 28

5. КОНТРОЛЬНЫЕ ВОПРОСЫ... 30

СПИСОК ЛИТЕРАТУРЫ... 31

 

1. моделирование непрерывных распределений

Большинство методов моделирования случайных величин на ЭВМ с различными законами распределения основано на использовании следующей теоремы:

Если случайная величина x имеет плотность распределения f(x), то распределение случайной величины y=F(x) является равномерным на интервале (0,1).

Здесь под F(x) понимается интегральная функция распределения случайной величины x.

Следовательно, можно поступить наоборот: построить функцию распределения F(x); выбрать случайное значение y из равномерного распределения в интервале (0,1) и определить то значение аргумента х, для которого F(x)=y.

Полученная таким образом случайная величина x будет иметь заданную функцию распределения F(x).

Эта же задача может быть решена не только графическими построениями, но и рядом других способов. В частности, аналитический способ основан на обратном преобразовании x=F ^–1(y), где F ^–1 – функция, обратная F.

Это преобразование сводится к решению интегрального уравнения относительно x_i

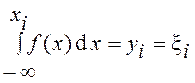                    ,                                               (1)

т.е. определяется такое значение x_i, при котором функция распределения равна y_i = ξ_i, где ξ_i  – значение случайной величины, равномерно распределенной на интервале (0,1).

В общем случае применение аналитических способов решения этого уравнения связано со значительным расходом машинного времени. Однако в частных случаях, когда решение уравнения (1) можно получить в явном виде, этот способ очень удобен.

Одним из наиболее экономных (по затратам машинного времени) методов получения случайных чисел с заданным законом распределения является способ кусочной аппроксимации плотности распределения f(x).

Сущность этого метода состоит в том, что область возможных значений случайной величины х разбивается на n интервалов, количество которых определяется точностью аппроксимации плотности распределения f(x). Левую границу k–го интервала обозначим а_k.

Будем считать, что в пределах интервала (а_k, а_k+1), значение функции f_k(x) не изменяется, тем самым мы заменяем кривую f(x) ступенчатой функцией.

Если случайным образом из n интервалов выбрать интервал (а_k, а_k+1), то получение случайного числа х_i с плотностью f(x) сводится к формированию равномерного распределения в интервале (а_k, а_k+1)

.                                         (2)