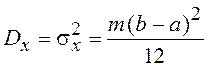Моделирование случайных величин. Методы генерирования на ЭВМ случайных величин с различными законами распределения, страница 4

.

Если а=0 и b=1, то

;     .

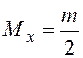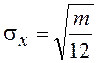Для получения последовательности нормально распределенных случайных чисел с заданными параметрами M_x,  представим случайную величину х в виде суммы

,                                                     (6)

где z_i – нормально распределенная случайная величина с параметрами M_z=0, .

Рассмотрим, как получить случайную величину z_i, располагая последовательностью равномерно распределенных в интервале (0, 1) случайных чисел . Согласно центральной предельной теореме имеем

.

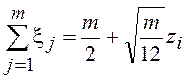Отсюда

.

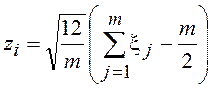Подставив значение z_i в (6), получим

.

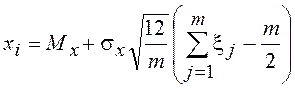Принимая m=12, находим

1.5. ЛОГАРИФМИЧЕСКИ НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ

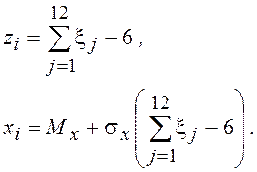
Плотность распределения вероятностей здесь имеет вид

               (7)

Рассмотрим способ формирования логарифмически нормального распределения, основанный на непосредственной связи распределения (7) с нормальным распределением. Действительно, если х – случайная величина, логарифм которой имеет нормальное распределение с параметрами , то справедливо соотношение

                              ,                                                        (8)

где z_i – нормально распределенная случайная величина с параметрами M_z=0, σ_z=1.

Отсюда

                              .                                                   (9)

Следовательно, формирование логарифмически нормального распределения сводится к получению нормированной случайной величины z_i и вычислению x_i согласно формулы (9).

1.6. гамма – распределение

Плотность распределения вероятностей для этого закона имеет вид

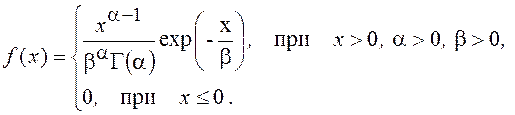
Математическое ожидание и дисперсия здесь равны

При целом  – это распределение Эрланга (см. ниже).

При  значения x получают следующим образом.

Пусть  – значения независимой случайной равномерно распределенной на интервале (0, 1) величины.

Вычислим

Если  то выбираем новую пару чисел , иначе определяем

.

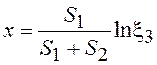Для произвольных  

где [] – целая часть числа .

Кроме распределения Эрланга, частными случаями гамма–распределения являются (хи–квадрат) (при β=2 и значениях α, кратных 1/2) и экспоненциальное ( при ) распределения.

1.7. РАСПРЕДЕЛЕНИЕ ЭРЛАНГА

Плотность распределения вероятностей для этого закона имеет вид

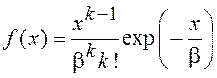, где k принимает только целочисленные значения (k=1, 2, …).

Математическое ожидание и дисперсия здесь равны

Распределение Эрланга непосредственно связано с распределением Пуассона: если начать измерение времени в момент совершения n–го события, то случайная величина x является длительностью интервала между n–ым и n+k–ым событием пуассоновского процесса. Этот интервал равен сумме k подинтервалов, каждый из которых является случайной величиной, имеющей экспоненциальное распределение с интенсивностью .

Отсюда следует, что случайная величина х, имеющая распределение Эрланга k–го порядка, может быть получена в виде суммы k случайных величин, имеющих экспоненциальное распределение,

1.8. РАСПРЕДЕЛЕНИЕ хи–квадрат

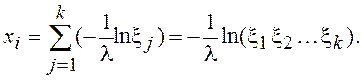
Плотность распределения вероятностей этого закона описывается выражением

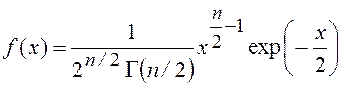, где n – число степеней свободы, Г(n/2) – гамма функция.

Математическое ожидание и дисперсия здесь равны

Формирование распределения (хи–квадрат) на ЭВМ основано на предельной теореме:

Сумма квадратов n независимых нормально распределенных случайных величин с математическим ожиданием m=0 и дисперсией  имеет распределение  с n степенями свободы.

Следовательно, процедура получения –распределения сводится к двукратному преобразованию:

·  Из равномерного распределения формируется последовательность n независимых нормально распределенных случайных величин  с параметрами  по формуле

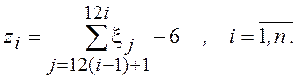
·  Производится суммирование квадратов, полученных случайных величин .

Величина

имеет –распределение с n степенями свободы.

1.9. РАСПРЕДЕЛЕНИЕ СТЬЮДЕНТА