В математической статистике это распределение называется иногда распределением t с k степенями свободы, так как описывает случайную величину
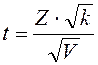 , (10)
, (10)
где Z и V – независимые случайные величины,
причем Z распределена нормально с параметрами Mz = 0 и Dz = 1, а V подчиняется закону ![]() с k степенями свободы.
с k степенями свободы.
Плотность вероятностей величины t имеет вид
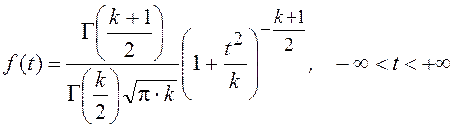 , (11)
, (11)
где Г( ) – гамма функция.
Математическое ожидание и дисперсия случайной величины t равны
![]()
То обстоятельство, что случайная величина t связана функциональной зависимостью (10) с другими случайными величинами, законы распределения которых известны, дает простой способ формирования распределения (11). Для этого необходимо:
· Получить реализацию нормально распределенной случайной величины Z с параметрами mz = 0, Dz = 1
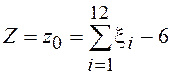 .
.
·
Сформировать реализацию случайной величины V, подчиненной ![]() –распределению:
–распределению:
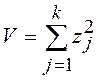 .
.
· Выполнить вычисления согласно формуле (10).
Таким образом получаем
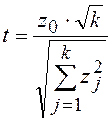 .
.
Это распределение широко используется в дисперсионном анализе. Оно описывает случайную величину
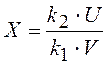 , (12)
, (12)
которая функционально
связана с двумя случайными величинами U и V, имеющими ![]() –распределения
с k1 и k2 степенями свободы соответственно.
–распределения
с k1 и k2 степенями свободы соответственно.
Плотность вероятности этого закона имеет вид
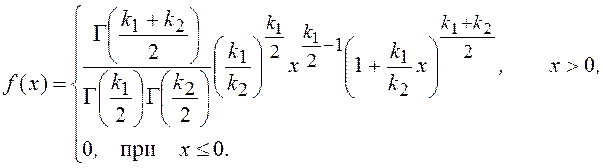
Математическое ожидание и дисперсия для этого закона равны
![]()
Для реализации случайной величины x, подчиненной распределению Фишера, необходимо, очевидно, сформировать
две случайные величины U и V, подчиненные ![]() –распределению
с k1 и k2 степенями свободы, и воспользоваться
формулой (12). Тогда получим
–распределению
с k1 и k2 степенями свободы, и воспользоваться
формулой (12). Тогда получим
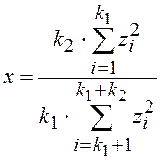 , где zi – значения нормально
распределенной случайной величины с
, где zi – значения нормально
распределенной случайной величины с ![]() .
.
Плотность распределения вероятностей этого закона имеет вид
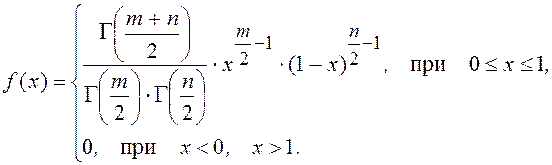 (13)
(13)
Математическое ожидание и дисперсия этого закона равны
![]()
Для случайной величины, имеющей бета–распределение, можно записать:
![]()
где ![]()
![]() –
случайная величина, имеющая хи–квадрат распределение.
–
случайная величина, имеющая хи–квадрат распределение.
Так как
![]() , то для реализации
случайной величины x, подчиненной распределению
(13), необходимо сформировать две случайные величины, имеющие
, то для реализации
случайной величины x, подчиненной распределению
(13), необходимо сформировать две случайные величины, имеющие ![]() –распределение с m и m+n степенями свободы, а затем получить
–распределение с m и m+n степенями свободы, а затем получить
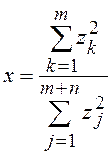 .
.
Плотность вероятностей распределения Вейбулла имеет вид
![]() , где
, где ![]() – масштабный параметр; k – параметр,
определяющий асимметрию и эксцесс.
– масштабный параметр; k – параметр,
определяющий асимметрию и эксцесс.
Математическое ожидание и дисперсия здесь равны
![]()
Для получения этого распределения может быть непосредственно использовано соотношение
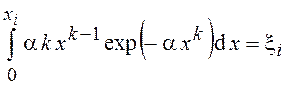 .
.
Нижний предел интегрирования равен 0, а не ![]() , так как область существования x
ограничена
, так как область существования x
ограничена ![]() .
.
Используя замену переменной, получаем
![]() .
.
Отсюда
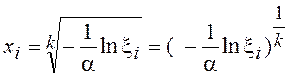 .
.
Распределение Релея является частным случаем
рассмотренного выше распределения Вейбулла. Действительно, при 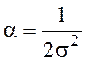 и k = 2 получим
и k = 2 получим
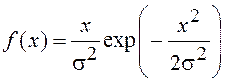 , (14)
, (14)
где s – параметр распределения Релея.
Для получения случайных чисел, распределенных по закону (14), справедливо соотношение
![]() .
.
Дискретные распределения случайных величин применяют для описания поведения случайных событий.
Алгоритм моделирования на ЭВМ случайных событий с известным законом распределения вероятностей сводится к следующему.
Пусть заданы значения вероятностей P1, P2,…, Pn для независимых событий A1, A2,…, An, образующих полную группу. Нужно определить в каждом испытании, какое из этих событий произошло.
Разобьем отрезок [0,1] на n отрезков так, чтобы длина i–го отрезка
равнялась вероятности Pi. Выберем из равномерного в интервале (0,1) распределения случайное
число ![]() и определим, на
какой участок попадает это число. Попадание случайного числа
и определим, на
какой участок попадает это число. Попадание случайного числа ![]() на k–й участок фиксируем как факт свершения события Ak . На ЭВМ этот
процесс сводится к выбору случайного числа
на k–й участок фиксируем как факт свершения события Ak . На ЭВМ этот
процесс сводится к выбору случайного числа ![]() и проверке условия
и проверке условия
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.