Моделирование случайных величин. Методы генерирования на ЭВМ случайных величин с различными законами распределения, страница 8

Наличие или отсутствие начального неслучайного участка можно определить на основе анализа нормированной автокорреляционной функции, описывающей взаимосвязь элементов статистической последовательности, так как для случайной последовательности эта функция близка к нулю.

Первые две проверки имеют смысл только для случайных совокупностей без начального неслучайного участка, поэтому проверку качества сгенерированной последовательности целесообразно начать с анализа нормированной автокорреляционной функции.

3.2. ОПРЕДЕЛЕНИЕ И АНАЛИЗ НОРМИРОВАННОЙ АВТОКОРРЕЛЯЦИОННОЙ ФУНКЦИИ

Нормированная автокорреляционная функция вычисляется по формуле

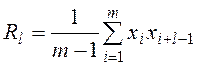,                                              (17)

где

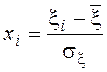
- центрированное и нормированное значение случайной величины ;

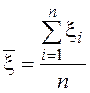
- оценка математического ожидания случайной величины ;

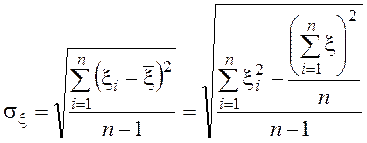
– оценка среднеквадратического отклонения случайной величины ;

n – число элементов в анализируемой последовательности;

m=n–l+1 –  при исследовании автокорреляционной функции индекс l увеличивается до тех пор, пока R_l не станет примерно равной 0.

По абсолютному значению R_l не превосходит 1. Причем, если последовательность достаточно случайна, R_l стремится к нулю с ростом l.

О значимости связи элементов последовательности можно судить по абсолютному значению .

Если с некоторого значения  выполняется условие

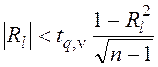
то, начиная с этого l, связь между элементами последовательности отсутствует.

Здесь  – коэффициент, определяемый по таблице распределения Стьюдента (см. табл. 2) для критерия значимости q (обычно q=0.1, 0.05, 0.01) и  степеней свободы.

Таблица 2

Значения распределения Стьюдента

	q				q
	0.10	0.05	0.01		0.10	0.05	0.01
1	6.314	12.706	63.657	12	1.812	2.179	3.055
2	2.920	4.303	9.925	14	1.782	2.145	2.977
3	2.353	3.182	5.841	16	1.761	2.120	2.921
4	2.132	2.776	4.604	18	1.746	2.101	2.878
5	2.015	2.571	4.032	20	1.734	2.086	2.845
6	1.943	2.447	3.707	22	1.725	2.074	2.819
7	1.895	2.365	3.499	24	1.717	2.064	2.797
8	1. 860	2.306	2.355	26	1.711	2.056	2.779
9	1.833	2.262	3.250	28	1.706	2.048	2.763
10	1.812	2.228	3.169	30	1.697	2.042	2.750

При  значения  не зависят от  и равны значениям, приведенным в табл. 3.

Таким образом, начиная с числа с номером n_нач, последовательность генерируемых чисел достаточно случайна.

                                                                            Таблица 3

Вот еще два способа определения начального участка, где последовательность генерируемых чисел нельзя считать случайной.