Построение моделей временных рядов. Проведение первичного статистического анализа, страница 9

Остаточная сумма квадратов для кусочной модели [1]:

= + = 12,185

Соответствующее ей число степеней свободы составит:   

= 49

Сокращение остаточной дисперсии при переходе от единого уравнения тренда к кусочной модели можно определить следующим образом:

∆ESS = ESS³ – ESS = 38,135-12,185=25,95  0.

Число степеней свободы, соответствующее , будет равно:.

Найдем F–статистику по следующей формуле:

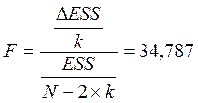 при k=3, N=55.                                                        (2.32)

F_kp (k, N-2*k)= F_kp(3,49) = 2,8

Так как , следовательно, гипотеза (о структурной стабильности ряда) отвергается при уровне значимости . Можно сделать вывод о том, что влияние структурных изменений на динамику изучаемого показателя признается значимым.

Таким образом, моделирование тенденции временного ряда, следует осуществлять с помощью кусочной модели (Рис.2.7).

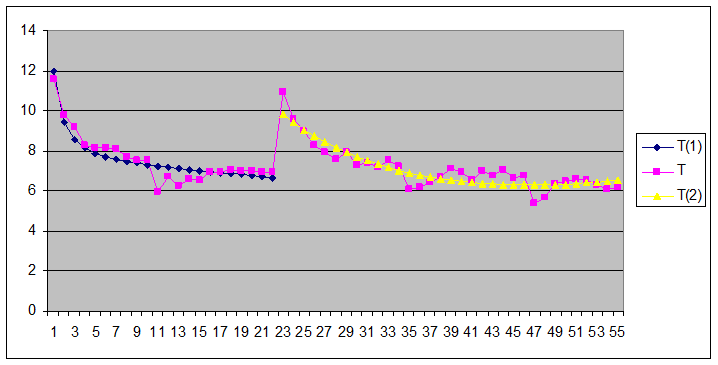
Рис. 2.7. Изменение характера тенденции временного ряда

Проверка ряда на наличие структурных изменений с помощью подхода Гуйарати [2].

Этот подход основан на использование фиктивной переменной, которая принимает два значения: 0 и 1.

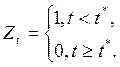                                                                                               (2.33)

Общее уравнение Гуйарати имеет вид:

Y_t =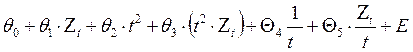

При

, где  - параметры 1-го уравнения.

При

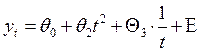 , где  - параметры 2-го уравнения

 - разница между свободными членами уравнений 1) и 2): если θ₁ – значимый, то изменение – значимо.

т.е. есть разница между параметрами θ₁₁ и θ₁₂ уравнений (1) и (2): если θ₃ – значимый, то изменение – значимо.

т.е. есть разница между параметрами θ₂₁ и θ₂₂ уравнений (1) и (2): если θ₅ – значимый, то изменение – значимо.

Оценка статистической значимости различий , а также  и эквивалентна оценке статистической значимости параметров уравнения Гуйарати.

Чтобы сделать проверку значимости сначала найдём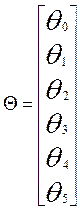  

t:1;2;…;55

T=X-S: 11,548;9,797 ;…;6,186.

Сделаем матричные обозначения и найдём .

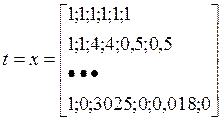
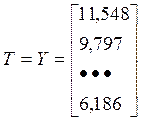
Оценка неизвестных параметров

Проверим значимость параметров ,  в каждом уравнении регрессии, используя критерий Стьюдента.

Выдвигаем гипотезы:

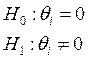
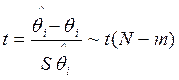                                                                                       (2.34)

                                                                                                   (2.35)

=

9,54176	-9,541758	-0,00212	0,002	-222,8	222,8
-9,5418	9,7793689	0,00212	-0,003	222,8	-223,2
-0,0021	0,0021197	5E-07	-5E-07	0,0483	-0,048
0,00212	-0,002806	-5E-07	3E-06	-0,048	0,049
-222,8	222,7983	0,04832	-0,048	5297,4	-5297
222,798	-223,2377	-0,04832	0,049	-5297	5299

                                                                                           (2.36)

S² = 0,2487

Таблица 2.12

Проверка значимости параметров уравнения

	Коэффициенты	Стандартная ошибка	t-статистика
	8,772	1,559	5,625
	-0,0022	9E-04	-2,446
	-248,33	36,3	-6,841

Таким образом, параметры ,, признаются значимыми.

В целом по подходу Гуйарати можно сделать вывод о влияние структурных изменений на динамику временного ряда и признание этого влияния значимым.

Прогнозирование значений месячного уровня осадков будем осуществлять по следующей модели:

X₁(t)=30,714+S_i+E

Результаты расчетов представлены в таблице 2.15.

Таблица 2.13

Расчет прогнозных значений Х₁