Построение моделей временных рядов. Проведение первичного статистического анализа, страница 6

Суммируем элементы ряда последовательно за каждые 12 месяцев со сдвигом на один момент времени.

Получаем: 98,6;93,3;…;92,9;…;76,7;76,1.

Разделив полученные суммы на 12, найдем скользящие средние:

8,217;7,775;…;7,742;…;6,392;6,342.

Приведем эти значения в соответствие с фактическими моментами времени, для чего найдем средние значения из двух последовательных скользящих средних – центрированные скользящие средние:

7,996;7,642;…;7,946;…;6,429;6,367.

Шаг 2. Расчет значений сезонной компоненты S.

Найдем оценки сезонной компоненты как разность между фактическими значениями ряда и центрированными скользящими средними.

Таблица 2.4

Расчет значений сезонной компоненты

год	месяц
	1	2	3	4	5	6	7	8	9	10	11	12
1	-	-	-	-	-	-	-1,796	0,058	0,304	1,871	0,775	-0,729
2	-1,038	0,237	-0,31	0,242	-0,242	-1,571	-2,404	-0,688	-0,717	0,6	4,933	1,183
3	0,558	0,733	-0,2	-0,537	-0,246	-1,7	-1,854	0,017	0,617	1,775	1,058	-1,071
4	-0,733	0,396	0,337	0,296	-0,354	-1,004	-1,679	0,533	0,263	1,8	0,825	-1,129
5	-0,366	-	-	-	-	-	-
	-0,395	0,456	-0,06	-9E-16	-0,281	-1,425	-1,933	-0,02	0,117	1,512	1,898	-0,436
	-0,348	0,503	0,01	0,047	-0,233	-1,378	-1,886	0,027	0,164	1,559	1,945	-0,389

 

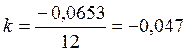
 =-                                                                                                   (2.18)

Шаг 3. Элиминируем влияние сезонной компоненты, вычитая ее значение из каждого значения исходного временного ряда. Получим: Т+Е = Х-S.

Таблица 2.5

Расчет выровненных значений Т

Шаг 4. Используя регрессионный анализ, проведем аналитическое выравнивание ряда Х-S. Построим функции тренда:

1) Т₁ =                          

Для нахождения используем метод наименьших квадратов:

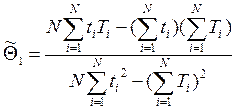                                                                           (2.19)

                                                                                 (2.20)

Получаем следующее уравнение: Т₁ =

Далее построим функцию значений линии тренда и найдем прогнозные значения .

Таблица 2.6

Расчет прогнозных значений для Т₁

Графически анализ прогноза для Т₁ представлен на рисунке 2.2.

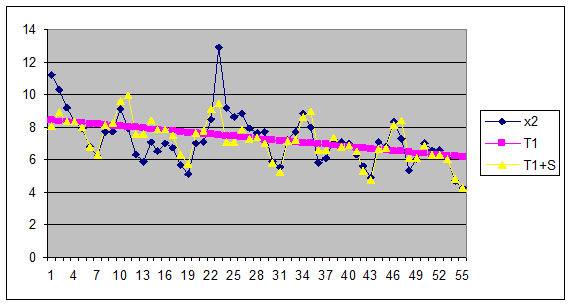
Рис. 2.2. Анализ  прогноза для Т₁

2) Т₂ =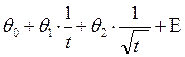

Построим матрицу значений независимых переменных.

Сделаем матричные обозначения:

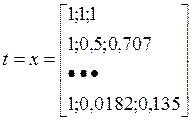
Оценка неизвестных параметров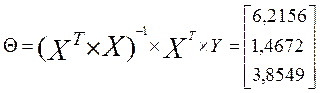

Далее построим функцию значений линии тренда и найдем прогнозные значения .  

Таблица 2.7

Расчет прогнозных значений для Т₂