Построение моделей временных рядов. Проведение первичного статистического анализа, страница 8

,                                                                                                  (2.28)

где q_ii – диагональные значения матрицы    

=

0,0651	-3,3022E-05	-0,1527
-3E-05	2,637E-08	6,8E-05
-0,1527	6,82759E-05	0,98112

S² – несмещенная оценка дисперсии случайной ошибки.

                                                                                           (2.29)  

S² = 0,733

Проверим значимость параметров ,,.

, =0,2186

,=0,00014

,=0,848

33,485

-2,7429

5,0303

t_кр= 2,0084

Вывод: Т.к. | t |> t_кр гипотеза Н₀ отвергается, значит все параметры данного уравнения являются значимыми.

2.2 Проверка остатков на автокорреляцию с помощью критерия Дарбина – Уотсона [5]

Модель временного ряда, описывающая месячный уровень осадков:

Х(Т)=30,714+S_i+E

Построим график остатков для данной модели (Рис.2.5).

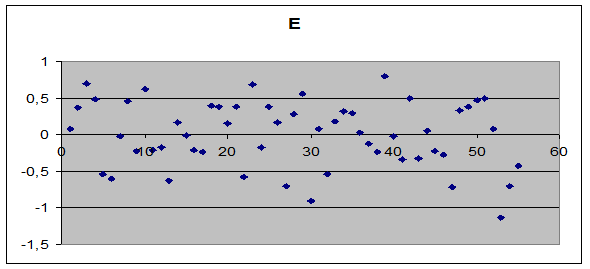
Рис.2.5. Остатки модели для Х₁

 

Анализ графика позволяет сделать вывод об отсутствие автокорреляции в остатках.

1) Выдвигаем гипотезы [1]:

Н₀: отсутствие автокорреляции в остатках;

Н₁: наличие положительной автокорреляции в остатках;

Н₁^*: наличие отрицательной автокорреляции в остатках.

2) Вычисляем статистику Дарбина-Уотсона:

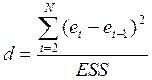                                                                                           (2.30)

3) По специальным таблицам определим критические значения статистики: d_L = 1,53; d_U = 1,60.

 

                           0          1,53       1,6        2,4        2,47       4

Значение статистики Дарбина-Уотсона попадает в промежуток [1,6; 2,4],значит, гипотеза Н₀  не отвергается. Можно сделать вывод, что в остатках отсутствует  автокорреляция.

Наилучшей моделью временного ряда, описывающей среднемесячные удои молока, является модель:

Т₃ =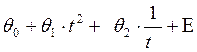 

Представим графически остатки, вычисленные по модели (Рис.2.6).

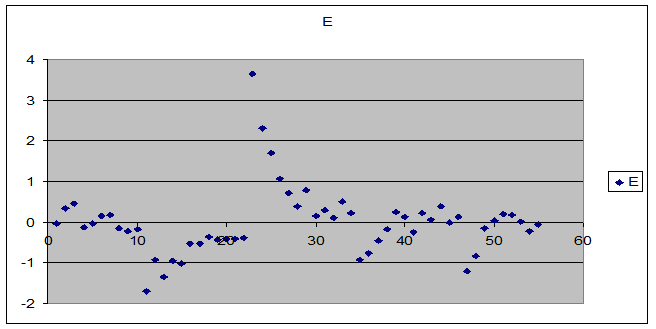
Рис.2.6. Остатки модели для Х₂

Шаг 1. Выдвигаем гипотезы [1]:

 - об отсутствии автокорреляции в остатках.

 - о наличии положительной автокорреляции в остатках.

 - о наличии отрицательной автокорреляции в остатках.

Шаг 2. Вычисление статистики Дарбина - Уотсона.

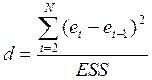                                                                                           (2.31)

Шаг 3. Определение критических значений  статистики Дарбина - Уотсона.

d_L = 1,45               d_U = 1,68   

 Шаг 4. Принятие решения об автокорреляции.

 

0           1,45      1,68      2,32      2,55         4

Значение d принадлежит интервалу (0; 1,45).Можно сделать вывод о том, что гипотеза Н₀ отвергается, в остатках наблюдается положительная автокорреляция.

2.3 Структурные изменения

На графике временного ряда, где показаны среднемесячные удои молока (рис.1.2.) предположительно наблюдаются структурные изменения в 23-ем месяце, т.к. именно в это время Робинзон огородил новый участок, оставив старый участок для восстановления травяного покрова.

Поэтому выдвигаем гипотезу о наличии структурных изменений и проверяем ее с помощью теста Чоу и подхода Гуйарати [2].

Таким образом, точка  t*,  в которой наблюдается структурное изменение,  равна: t* = 23.

Проверка ряда на наличие структурных изменений с помощью теста Чоу.

Сформулируем гипотезы:

 структурная стабильность

структурное изменение.

1 уравнение: Т⁽¹⁾ =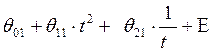 

t:1;2;…;22

T=X-S: 11,548; 9,797;…; 6,941.

Сделаем матричные обозначения и найдём ,,.

                     

           

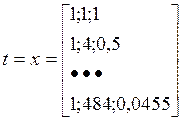
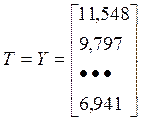
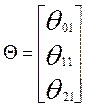
Оценка неизвестных параметров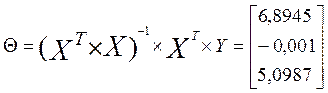

2 уравнение: Т⁽²⁾ =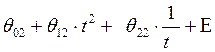 

t:23;24;…;55

T=X-S: 10,955; 9,589;…;6,186.

Сделаем матричные обозначения и найдём ,,.

                     

           

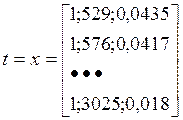
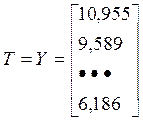
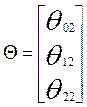
Оценка неизвестных параметров

В таблице 2.13 приведены расчеты по тесту Чоу.

Таблица 2.11

Тест Чоу