Построение моделей временных рядов. Проведение первичного статистического анализа, страница 3

7,22

Далее найдем дисперсию и меру разброса по формулам:

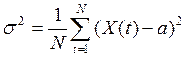                                                                                       (2.2)

                                                                                                           (2.3)

Получаем:

  18,155

  2,474

S_x1 =  4,261

S_x2 = 1,573

Таким образом, в среднем на необитаемом острове выпадает 30,48 миллиметров осадков, а среднемесячные удои молока составляют 7,22  галлонов. Значения месячного уровня осадков колеблются в пределах ± 4,261 миллиметров от среднего. Значения среднемесячных удоев молока варьируются в пределах  ± 1,573 галлонов от среднего.

На основе полученных данных можно предположить, что временные ряды уровня осадков и удоев, возможно, имеют периодический характер, поскольку значения обоих рядов отклоняются от среднего не значительно.

1.3 Вычисление автоковариационной и автокорреляционной функции. Построение коррелограммы

Найдем автоковариационную функцию, которая показывает зависимость между элементами временного ряда, сдвинутых по времени на величину , по формуле[2]:

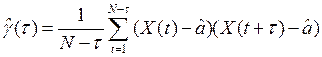,                                                               (2.4)

           где

Вычислим автоковариационную функцию для двенадцати значений месячного уровня осадков и среднемесячных удоев молока:

Таблица 2.1

Вычисление автоковариационной функции

	для Х1	для Х2
1	5,846	1,429
2	-4,389	0,580
3	-7,943	0,175
4	-7,209	-0,180
5	1,043	-0,025
6	9,722	0,343
7	1,035	0,015
8	-7,407	-0,376
9	-8,818	-0,167
10	-4,935	-0,184
11	5,4390	0,172
12	17,315	0,641

Вычислим автокорреляционную функцию месячного уровня осадков и среднемесячных удоев молока для 12 значений по формуле:

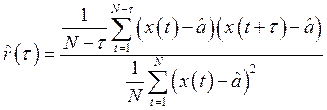                                                                  (2.5)

Таблица 2.2

Вычисление автокорреляционной функции

Построим коррелограмму для месячного уровня осадков (Рис.2.1).

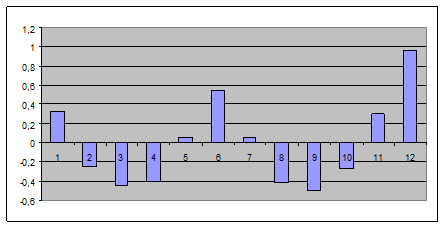
Рис.2.1. Коррелограмма месячного уровня осадков

Из построенной коррелограммы для месячного уровня осадков можно сказать о периодичности, т.е. сезонной зависимости уровня осадков. Также график показывает, что элементы ряда имеют большой разброс во времени, значит, элементы ряда слабо связаны друг с другом.

Построим коррелограмму для среднемесячных удоев молока (Рис.2.2).

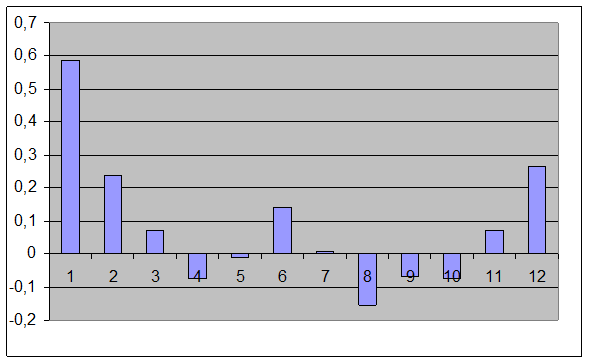
Рис.2.2. Коррелограмма среднемесячных удоев молока

Из построенной коррелограммы видно, что элементы временного ряда имеют небольшой разброс во времени, значит, элементы ряда связаны друг с другом. Также видно, что разброс значений автокорреляционной функции повторяется через некоторый период времени, что говорит о возможном присутствии сезонной компоненты.

2 ПОСТРОЕНИЕ МОДЕЛИ ВРЕМЕННОГО РЯДА

2.1 Построение модели для неслучайных компонент

Запишем основное разложение временного ряда. Т.к. амплитуда колебаний значений месячного уровня осадков постоянна, значит, будем строить аддитивную модель[1].

Проверим гипотезу о наличие/отсутствия сезонности в этом разложение:

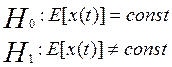
Для проверки этой гипотезы используют следующие критерии:

1.  Критерий серий.

2.  Критерий «восходящих» и «нисходящих» серий.