Построение моделей временных рядов. Проведение первичного статистического анализа, страница 5

                  

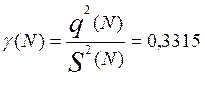
При больших N 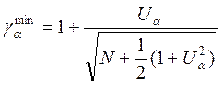                                                   (2.16)

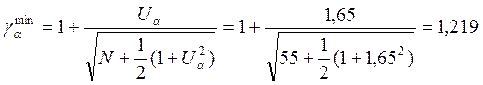
Т.к. , то гипотеза Н₀ отвергается. Значит, в разложении временного ряда присутствуют неслучайные компоненты, а именно – тренд и сезонность.

Построение моделей сводится к расчету значений Т, S, Е для каждого элемента временного ряда [4].

Шаг 1. Выравнивание исходного ряда методом скользящей средней.

Шаг 2. Расчет значений сезонной компоненты S.

Шаг 3. Устранение сезонной компоненты S и получение выровненных данных (T+S).

Шаг 4. Аналитическое выравнивание полученного ряда и расчет значений трендовой компоненты Т.

Шаг 5. Расчет прогнозных значений Х=Т+ S.

Шаг 6. Проверка адекватности модели.

Поскольку проверка гипотезы о наличие неслучайных компонент в разложении ряда показала, что во временном ряде месячного уровня осадков отсутствуют трендовая и сезонная компоненты. График же данного временного ряда подтверждает, что тренда нет. Но, возможно, временной ряд содержит сезонную компоненту, поскольку на графике прослеживается период, равный 12 месяцам. 

Построим модель для месячного уровня осадков.

Шаг 1. Выравнивание исходного ряда методом скользящей средней.

Суммируем элементы ряда последовательно за каждые 12 месяцев со сдвигом на один момент времени.

Получаем: 369,5; 368,8;…; 368,9;…;367;366,9.

Разделив полученные суммы на 12, найдем скользящие средние:

30,79; 30,73;…;30,74;…;30,58;30,575.

Приведем эти значения в соответствие с фактическими моментами времени, для чего найдем средние значения из двух последовательных скользящих средних – центрированные скользящие средние:

30,76;30,73;…;30,71;…;30,63;30,58.

Шаг 2. Расчет значений сезонной компоненты S.

Найдем оценки сезонной компоненты как разность между фактическими значениями ряда и центрированными скользящими средними.

Таблица 2.3

Расчет значений сезонной компоненты

год	месяц
	1	2	3	4	5	6	7	8	9	10	11	12
1	-	-	-	-	-	-	-7,663	2,375	1,413	9,271	4,787	-4,267
2	-3,625	1,671	-0,342	0,883	-0,004	-4,442	-7,283	1,975	1,904	7,913	5,458	-4,421
3	-2,654	1,688	-0,975	1,396	0,775	-5,717	-7,504	1,433	1,788	8,838	5,188	-4,133
4	-3,175	1,217	0,408	1,05	-0,083	-4,254	-7,888	1,963	1,346	8,254	4,183	-3,733
5	-2,479	-	-	-	-	-
	-2,983	1,525	-0,303	1,109	0,229	-4,804	-7,584	1,936	1,613	8,569	4,904	-4,139
	-2,989	1,519	-0,309	1,104	0,223	-4,81	-7,59	1,930	1,606	8,563	4,898	-4,144

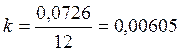
=-                                                                                                    (2.17)

Шаг 3. Устранение сезонной компоненты S и получение выровненных данных (T+S).

Вычитаем значение сезонной компоненты из каждого элемента исходного ряда.

Получаем X-S: 30,79;31,08;…;31,27;…;30,01;30,29.

Шаг 4. Найдем константу а, т.е.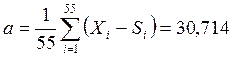

Шаг 5. Рассчитаем прогнозные значения  = a + S – значения уровней ряда, полученные по аддитивной модели и построим график данного временного ряда X(t) и(Рис.2.1).

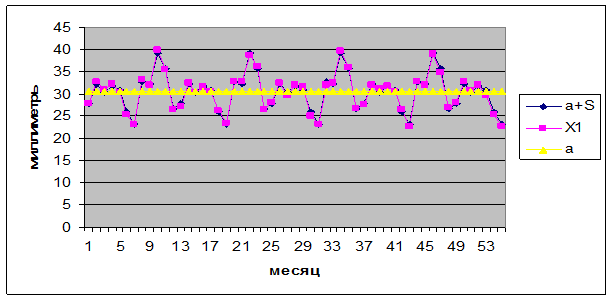
Рис.2.1. Прогнозные значения месячного уровня осадков

Для временного ряда среднемесячных удоев молока модель имеет вид:

                                                           X₂(t)=T(t)+S(t)+E(t)

Шаг 1. Выравнивание исходного ряда методом скользящей средней.