Построение моделей временных рядов. Проведение первичного статистического анализа, страница 7

Графически анализ прогноза для Т₂ представлен на рисунке 2.3.

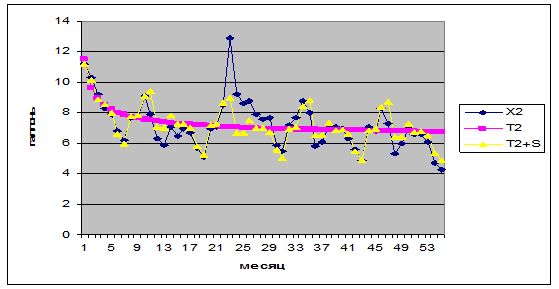
Рис. 2.3. Анализ  прогноза для Т₂

3)Т₃ =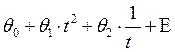 

Сделаем матричные обозначения:

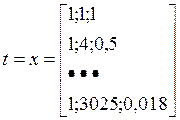
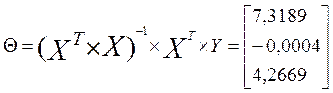
Далее построим функцию значений линии тренда и найдем прогнозные значения .

Таблица 2.8

Расчет прогнозных значений для Т₃

Графически анализ прогноза для Т₃ представлен на рисунке 2.4.

Рис. 2.4. Анализ  прогноза для Т₃

Для того чтобы выбрать наилучшую функцию тренда нужно вычислить коэффициент детерминации и проверить значимость уравнения по F-критерию[5].

Шаг 1. Проверка адекватности модели (расчет остатков Е = Х – (Т_i+S)).

Таблица 2.9

Расчет остатков для трех моделей

Е = Х – (Т1+S)	Е = Х – (Т2+S)	Е = Х – (Т3+S)
3,142	0,0099	-0,0377
1,434	0,122	0,3465
0,888	0,279	0,472
-0,0274	-0,257	-0,1266
-0,1051	-0,0996	-0,0293
…	…	…
0,288	-0,174	0,1994
0,273	-0,226	0,183
0,0952	-0,439	0,0055
-0,1187	-0,6895	-0,208
0,031	-0,576	-0,0564

Шаг 2. Вычисление коэффициента детерминации.

,                                                                                       (2.21)

где    TSS – общая сумма квадратов

         ESS – остаточная сумма квадратов

         RSS – объясненная сумма квадратов

                                                                                           (2.22)

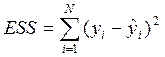                                                                                         (2.23)

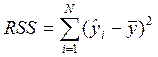                                                                                          (2.24)

                                                              Таблица 2.10

Вычисление коэффициента детерминации

	Т1	Т2	Т3
ESS	53,91	42,023	38,135
RSS	24,069	35,956	39,844
TSS	77,979	77,979	77,979
R2	0,309	0,461	0,51

Шаг 3. Проверка значимости регрессионных уравнений по F – критерию[6].

Выдвигаем гипотезу:

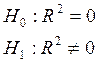
1) Для Т₁ =

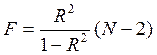                                                                                           (2.25)

F=23,66

= 4

Т.к. F>F_кр, гипотеза Н₀ отвергается, уравнение хорошего качества.

2) Для Т₂ =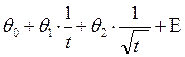

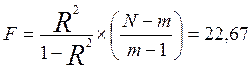                                                                        (2.26)

F_кр= 3,23

Т.к. F>F_кр, гипотеза Н₀ отвергается, уравнение хорошего качества.

3) Для  Т₃ = 

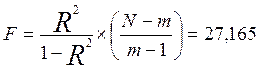
F_кр= 3,23

Т.к. F>F_кр, гипотеза Н₀ отвергается, уравнение хорошего качества.

Вывод: Наиболее значимым является уравнение Т₃ =  , т.к. коэффициент детерминации для данного уравнения равен 0,51.

Шаг 4. Проверка значимости параметров уравнения [2].

Т₃ =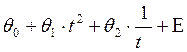 

1) Выдвигаем гипотезу: Н₀:  = 0

                                          Н₁:  ≠ 0

2)Сформулируем критическую статистику:

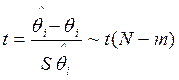,                                                                                     (2.27)

где -оценка неизвестного параметра ,

      - оценка среднеквадратического отклонения оценки .