3. Критерий Абеля.
Проверим гипотезу с помощью критерий серий[3].
1) Расположим элементы данного временного ряда в порядке возрастания Х1: 22,7; 22,8;…;31,2;…;39,6;39,9.
2) Вычислим выборочную медиану
 (2.1)
(2.1)
В данном случае, N=55 –
нечетно. Значит, ![]()
3) Получаем серию знаков «+» и «- » по правилу:
Вместо каждого элемента временного ряда нужно поставить:
«+», если ![]()
«-», если ![]()
На основание «+» и «- » вычисляем количество
серий (![]() ) и
длину максимальной серии (
) и
длину максимальной серии (![]() ).
).
![]() = 27
= 27
![]() = 4
= 4
3) Критерий проверки гипотезы опирается на две статистики:
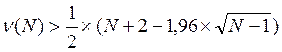 (2.2)
(2.2)
![]() (2.3)
(2.3)
Итак, 27>21,3 и 4<5,756.
Следовательно, в данном временном ряде отсутствует такая компонента как тренд, поскольку данный критерий наилучшим образом позволяет определить наличие трендовой компоненты.
Этот критерий улавливает постепенное смещение среднего значения не только монотонного, но и периодического характера.
1) Анализируем последовательность знаков «+» и «- » по правилу:
поставить «+», если ![]()
«-», если ![]()
Количество серий (![]() ) = 34
) = 34
Длина максимальной серии (![]() ) = 3
) = 3
2) Приближенное правило проверки:
 (2.4)
(2.4)
![]() ,
(2.5)
,
(2.5)
где
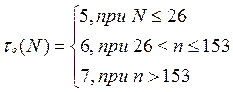 (2.6)
(2.6)
Итак, 34>30,31 и 3<6 – значит, гипотеза Н0 не отвергается, следовательно, в разложение временного ряда отсутствует сезонная компонента.
Проверим гипотезу с помощью критерия Абеля [5].
Вычислим:
 (2.7)
(2.7)
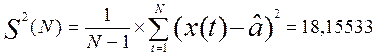 (2.8)
(2.8)
 (2.9)
(2.9)
При больших N  ,
(2.10)
,
(2.10)
где ![]() - квантиль стандартного нормального распределения.
- квантиль стандартного нормального распределения.
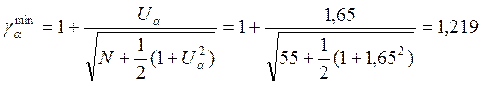
Т.к. ![]() ,
то гипотеза Н0 отвергается. Значит, в разложении временного ряда
присутствуют неслучайные компоненты.
,
то гипотеза Н0 отвергается. Значит, в разложении временного ряда
присутствуют неслучайные компоненты.
На основе выводов, сделанных во второй главе, можно записать основное разложение временного ряда для среднемесячных удоев молока:
![]()
Проверим гипотезу о наличии/отсутствия тренда и сезонности в разложении временного ряда.
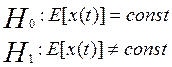
1) Расположим элементы данного временного ряда в порядке возрастания Х2:4,3;4,7;…;7,1;…;11,2;12,9 .
2) Вычислим выборочную медиану:
 (2.11)
(2.11)
В данном случае, N=55 –
нечетно. Значит, ![]()
3) Получаем серию знаков «+» и «-» по правилу:
Вместо каждого элемента временного ряда нужно поставить:
«+», если ![]()
«-», если ![]()
На основание «+» и «-» вычисляем количество
серий (![]() ) и
длину максимальной серии (
) и
длину максимальной серии (![]() ).
).
![]() = 10
= 10
![]() = 8
= 8
4) Пользуясь формулами (2.2) и (2.3), вычисляем две статистики для проверки гипотезы.
Итак, 10<21,3 и 8 >5,756.
Делаем вывод о том, что в разложении временного ряда присутствует трендовая составляющая.
Проверим гипотезу с помощью критерия «восходящих» и «нисходящих» серий.
1) Анализируем последовательность знаков «+» и «-» по правилу:
поставить «+», если ![]()
«-», если ![]()
Количество серий (![]() ) = 23
) = 23
Длина максимальной серии (![]() ) =5
) =5
2)Приближенное правило проверки:
 (2.12)
(2.12)
![]() ,
,
где
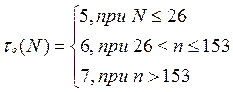 (2.13)
(2.13)
Итак, 23<30,31 и 5<6 – значит, в разложении временного ряда присутствует сезонная компонента.
Проверим гипотезу с помощью критерия Абеля.
Вычислим:
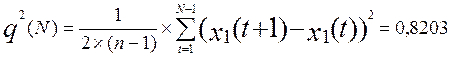 (2.14)
(2.14)
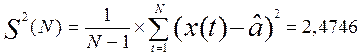 (2.15)
(2.15)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.