Конспект лекционных и практических занятий по дисциплине "Сопротивление материалов", страница 9

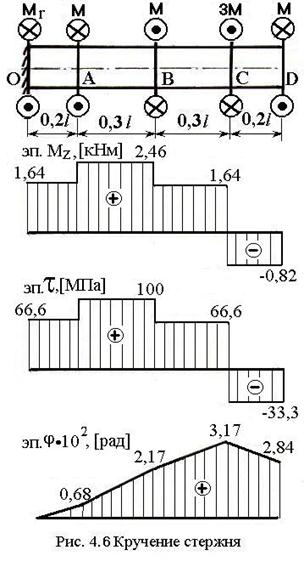
1) построить эпюру крутящих моментов

2) построить эпюру касательных напряжений

3) определить грузоподъемность  из условия прочности по касательным напряжениям

4) построить эпюру углов закручивания

Решение.

Заменяя жесткую заделку на реактивный момент , и совмещая начало координат с неподвижным концом вала, составляем сумму проекций всех моментов на ось вала:

 (реактивный момент в заделке направлен в ту же сторону, что и на рисунке).

Выражение для крутящих моментов имеет вид (для 4-х участков вала):

Поскольку вал имеет постоянное поперечное сечение по всей длине, то полярный момент сопротивления также постоянен и для сплошного вала равен

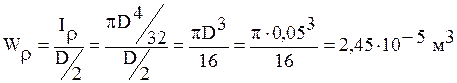, а жесткость стержня на кручение равна

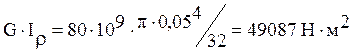
Выражения для касательных напряжений для каждого из участков :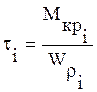

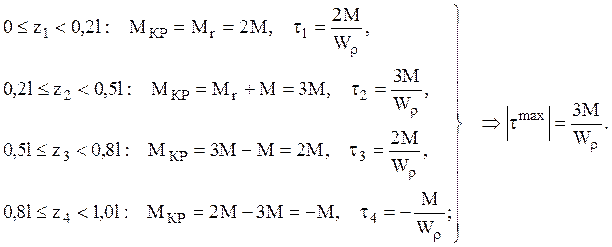
3) Условие прочности при чистом кручении:

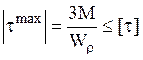
Определяем грузоподъемность

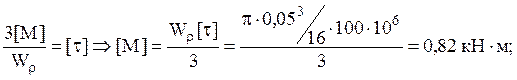
Записываем выражение для крутящего момента в числовом виде:

 и строим эпюру.

Определяем значения касательных напряжений для найденного максимального значения крутящего момента:

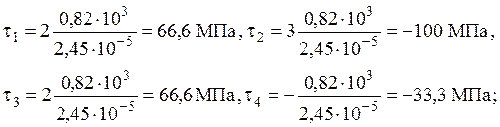
Определяем углы закручивания вала

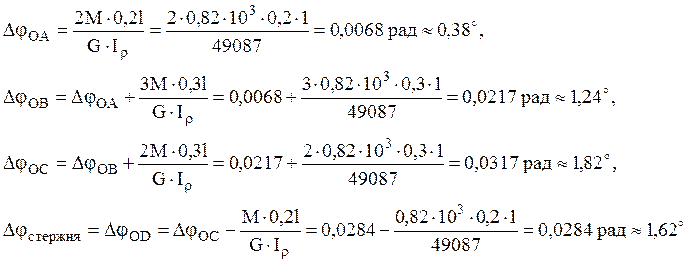
Строим эпюру углов закручивания, которая является кусочно-линейной функцией.

5. Изгиб прямых стержней

5.1 Основные допущения

Гипотеза о ненадавливании продольных волокон: волокна стержня, параллельные его оси, испытывают деформацию растяжения-сжатия в продольном направлении и не оказывают давления друг на друга в поперечном направлении. Данная гипотеза означает, что из всех нормальных напряжений присутствуют только , которые можно определить по закону Гука:  и каждое продольное сечение будет находиться в состоянии одноосного растяжения-сжатия.

Гипотеза плоских сечений: каждое поперечное сечение стержня плоское до деформации остается плоским и нормальным к искривленной оси стержня после деформации. Данная гипотеза на практике оказывается действительной для длинных стержней: если характерный размер поперечного сечения относится к длине  как.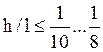

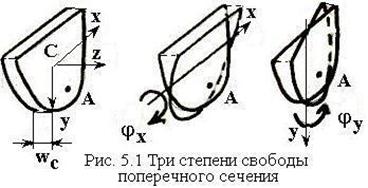При введении этих гипотез каждое поперечное сечение стержня будет являться абсолютно-жестким диском, имеющим три степени свободы (рис. 5.1).

Пусть перемещение , если оно направлено в положительном направлении оси , тогда перемещение произвольной точки сечения A имеет вид:

.

Правило знаков при изгибе:

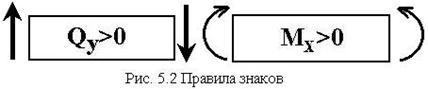Поперечная сила является положительной, если она поворачивает элемент по часовой стрелке. Изгибающий момент является положительным, если сжатые им волокна расположены сверху (рис.5.2).

Классификация изгибов:

Чистый изгиб – в поперечных сечениях стержня присутствует только изгибающий момент: ;

Поперечный изгиб – в поперечных сечениях стержня присутствует и изгибающий момент и поперечная сила: ;

Плоский изгиб – изгиб стержня в одной из главных плоскостей инерции:  или .

Косой изгиб – изгиб одновременно в двух главных плоскостях инерции: .

5.2 Плоский изгиб

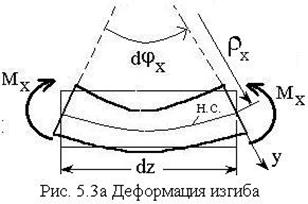Рассмотрим деформацию изгиба, выделив из деформированной балки бесконечно-малый элемент (рис.5.3а). Вследствие непрерывности деформации по высоте поперечного сечения будет существовать некоторый промежуточный слой материала, который искривляясь, сохраняет первоначальную длину . Такой слой материала называется нейтральным слоем, а линия пересечения нейтрального слоя с поперечным сечением называется нейтральной (нулевой) линией. При плоском изгибе нейтральная линия проходит через центр тяжести (). Определим продольную деформацию произвольного волокна удаленного от нейтрального слоя на расстояние : 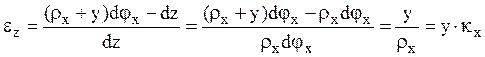, где  - радиус кривизны изогнутой оси в данной точке, а 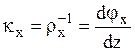 - кривизна в этой же точке. Таким образом, деформация по высоте сечения распределена по линейному закону.

Пусть во всех сечениях  (случай плоского изгиба в вертикальной плоскости), тогда 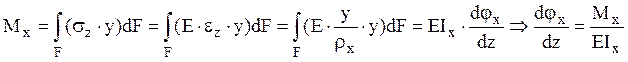 где  называется жесткостью поперечного сечения при изгибе в вертикальной плоскости. Тогда .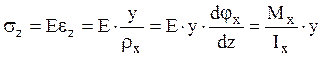

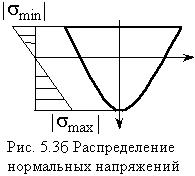Наибольшее нормальное напряжение при плоском изгибе возникает в точке (точках), наиболее удаленных от нейтральной линии (при ).

Условие прочности по нормальным напряжениям имеет вид: 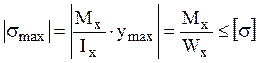, где  - момент сопротивления при изгибе. Для круга - 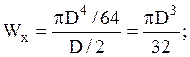 для прямоугольника -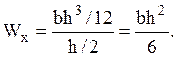

Продольная деформация меняется по высоте поперечного сечения по линейному закону 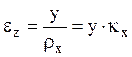, где  - радиус кривизны, а  - кривизна в данной точке.

5.3 Дифференциальные зависимости между внутренними усилиями при изгибе

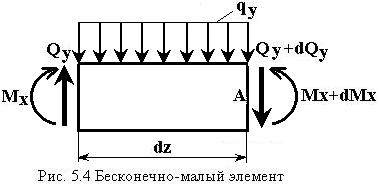Рассмотрим бесконечно-малый элемент стержня длиной  (рис. 5.4).  Составим условия равенства нулю всех сил относительно оси  и всех моментов относительно точки A:

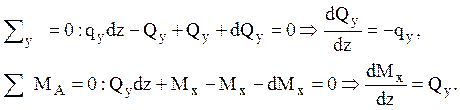
Отсюда следует важное соотношение между изгибающим моментом и поперечной силой:

1)  если на каком-то участке поперечная сила положительна, то изгибающий момент на этом участке возрастает;

2)  если на каком-то участке поперечная сила отрицательна, то изгибающий момент на этом участке убывает;

3)  если в какой-то точке поперечная сила равна нулю, то изгибающий момент в этой точке имеет экстремум;

4)  если поперечная сила равна нулю на каком-то участке, то изгибающий момент на этом участке постоянен;

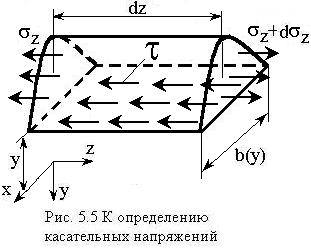
5.4 Определение касательных напряжений

Пусть стержень имеет постоянное поперечное сечение. Вырежем из стержня сектор, ограниченный горизонтальным сечением на произвольном расстоянии  от нейтральной линии и поперечными сечениями, удаленными друг от друга на бесконечно-малое расстояние , и рассмотрим все напряжения, действующие по его граням (рис. 5.5).

Гипотеза: по ширине сечения  касательные напряжения распределены равномерно.

Полагая, что формула для определения нормальных напряжений 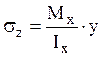 действительна, составим уравнение равновесия всех сил на ось стержня:

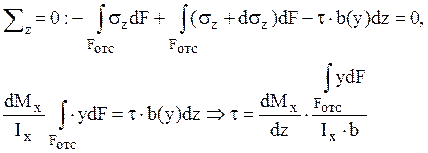
Интеграл берется по отсеченной площади поперечного сечения (расположенной выше линии сечения) и равен статическому моменту этой площади относительно нейтральной оси 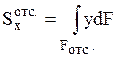, а 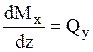, тогда 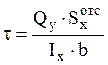. Данное выражение называется формулой Д. И. Журавского и выполняется точно, вследствие принятой гипотезы, только для тонкостенных сечений.