Неизвестные начальные параметры ![]() определяются из граничных условий,
составленных для левого и правого концов стержня. В случае наличия у стержня
промежуточных опор для определения действующих на них реактивных усилий
составляются дополнительные условия отсутствия прогибов на них, а неизвестная
реакция на опоре учитывается в качестве слагаемого соответствующего силе. При
построении эпюр поперечных сил и изгибающих моментов в местах действия
соответствующих сосредоточенных усилий происходят скачки. Кроме того, следует
проверять выполнение дифференциальных соотношений между внутренними усилиями.
Вследствие степенной зависимости от осевой координаты эпюры прогибов и углов
поворота являются гладкими функциями, не имеющими скачков и изломов. В точках,
где сила равна нулю, момент имеет экстремум, а в точках, где момент равен нулю,
кривизна изогнутой оси равна нулю, т.е. имеется точка перегиба.
определяются из граничных условий,
составленных для левого и правого концов стержня. В случае наличия у стержня
промежуточных опор для определения действующих на них реактивных усилий
составляются дополнительные условия отсутствия прогибов на них, а неизвестная
реакция на опоре учитывается в качестве слагаемого соответствующего силе. При
построении эпюр поперечных сил и изгибающих моментов в местах действия
соответствующих сосредоточенных усилий происходят скачки. Кроме того, следует
проверять выполнение дифференциальных соотношений между внутренними усилиями.
Вследствие степенной зависимости от осевой координаты эпюры прогибов и углов
поворота являются гладкими функциями, не имеющими скачков и изломов. В точках,
где сила равна нулю, момент имеет экстремум, а в точках, где момент равен нулю,
кривизна изогнутой оси равна нулю, т.е. имеется точка перегиба.
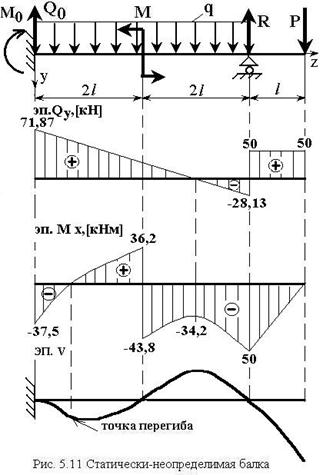
5.8 Пример раскрытия статической неопределимости балки с помощью уравнения изогнутой оси
Для балки (см.рис.5.11) при ![]() .
.
1) записать уравнение изогнутой оси
2)  определить
неизвестные начальные параметры из граничных условий
определить
неизвестные начальные параметры из граничных условий
3) получить выражения и построить эпюры поперечных сил и изгибающих моментов
4) построить изогнутую ось балки
Решение.
Совмещаем начало координат с левым концом балки
1. Уравнение изогнутой оси балки
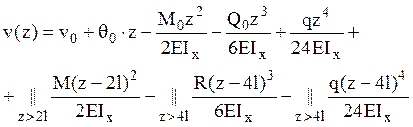 .
.
Cоставляем граничные условия
при ![]() :
: ![]()
при ![]() :
: ![]()
при ![]() :
: ![]()
Положив в универсальном уравнении ![]() выражения для силы и момента, получим
дифференцированием
выражения для силы и момента, получим
дифференцированием
![]()
![]() .
.
Решая систему уравнений
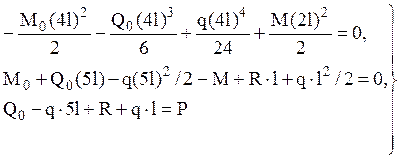
получим ![]() .
.
Подставив найденные значения начальных параметров в их выражения, определим их значения в характерных точках:

Определяем абсциссу на втором участке балки,
где поперечная сила равна нулю 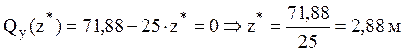 , при этом
, при этом ![]() имеет максимум.
имеет максимум.
По полученным значениям строим эпюры
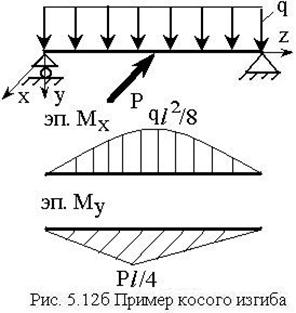
5.9 Косой изгиб
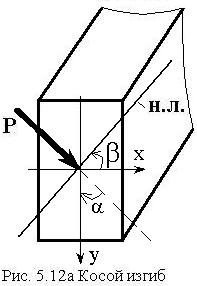 В случае, если плоскость действия
нагрузок не совпадает с главной осью сечения изгиб будет косым
(рис.5.12а). При этом в поперечных сечениях стержня будут присутствовать два
изгибающих момента, т.е. косой изгиб можно представить в виде сочетания двух
изгибов в главных плоскостях. У круглого и квадратного сечения все оси,
проведенные через центр тяжести, являются главными и поэтому такие балки
испытывают только плоский изгиб.
В случае, если плоскость действия
нагрузок не совпадает с главной осью сечения изгиб будет косым
(рис.5.12а). При этом в поперечных сечениях стержня будут присутствовать два
изгибающих момента, т.е. косой изгиб можно представить в виде сочетания двух
изгибов в главных плоскостях. У круглого и квадратного сечения все оси,
проведенные через центр тяжести, являются главными и поэтому такие балки
испытывают только плоский изгиб.
Следовательно, в выражении для нормальных
напряжений остаются два слагаемых: 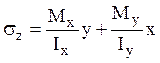 . Нейтральная
линия при этом проходит через центр тяжести сечения, но не перпендикулярна
плоскости действия нагрузок:
. Нейтральная
линия при этом проходит через центр тяжести сечения, но не перпендикулярна
плоскости действия нагрузок: 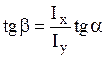 , где
, где ![]() - угол наклона плоскости действия
сил к главной оси. Перемещения при косом изгибе находятся в плоскости,
составляющей угол
- угол наклона плоскости действия
сил к главной оси. Перемещения при косом изгибе находятся в плоскости,
составляющей угол ![]() с главной осью.
с главной осью.
Наибольшие нормальные напряжения возникают в
точках сечения, наиболее удаленных от нейтральной линии: 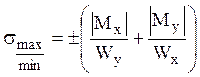 .
.
Условием прочности при косом изгибе является 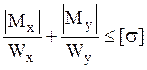 .
.
Пример. Подобрать поперечное сечение для
балки, подвергающейся косому изгибу, при ![]() (рис. 5.12б).
(рис. 5.12б).
Решение:
 Наибольшие значения моментов равны
Наибольшие значения моментов равны 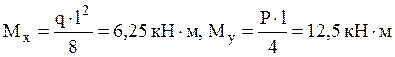 .
.
Рассмотрим несколько видов сечений:
а) прямоугольник с отношением высоты к ширине
![]() . Тогда
. Тогда 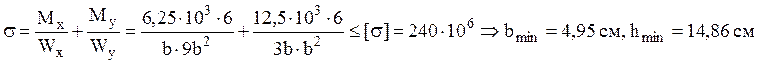 .
.
Площадь такого сечения равна ![]() .
.
б) круг с отношением внутреннего диаметра к
наружному ![]() .
.
Поскольку балки с таким сечением не испытывают косого изгиба то в расчет должен приниматься суммарный момент:
Тогда 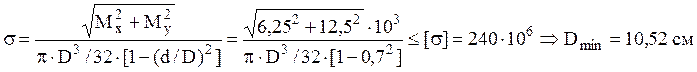 .
.
Площадь такого сечения равна ![]() .
.
в) двутавр
Принимаем двутавр №33, у которого ![]() .
.
Тогда 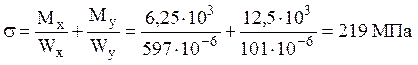 .
.
5.10 Внецентренное растяжение (сжатие)
Если линия действия осевой силы параллельна геометрической оси стержня, но не совпадает с ней, то такой случай нагружения стержня называется внецентренным растяжением (сжатием).
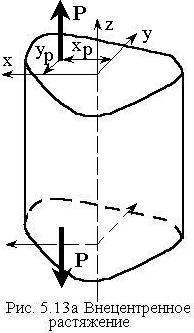 Пусть координаты точки приложения силы
Пусть координаты точки приложения силы
![]() (рис. 5.13а), тогда возникающие при
этом внутренние усилия равны
(рис. 5.13а), тогда возникающие при
этом внутренние усилия равны ![]() . Таким образом,
данный вид нагружения является сочетанием осевого растяжения ( или сжатия) и
косого изгиба (или изгибов в двух главных плоскостях). Выражение для нормальных
напряжений имеет наиболее общий вид:
. Таким образом,
данный вид нагружения является сочетанием осевого растяжения ( или сжатия) и
косого изгиба (или изгибов в двух главных плоскостях). Выражение для нормальных
напряжений имеет наиболее общий вид:
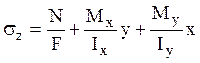 или в данном
случае
или в данном
случае 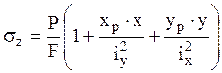 , где
, где 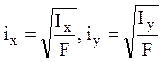 -
радиусы инерции площади поперечного сечения. Приравняв выражение для нормальных
напряжений нулю, получим уравнение нейтральной линии:
-
радиусы инерции площади поперечного сечения. Приравняв выражение для нормальных
напряжений нулю, получим уравнение нейтральной линии: 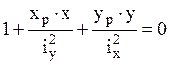 .
.
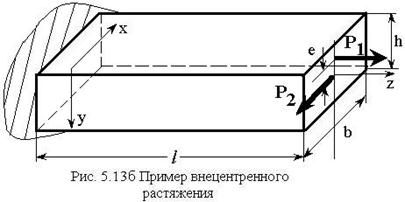
Пример. Консоль прямоугольного поперечного
сечения ![]() растягивается силой
растягивается силой ![]() , приложенной с эксцентриситетом
, приложенной с эксцентриситетом ![]() относительно оси
относительно оси ![]() и изгибается силой
и изгибается силой ![]() (рис. 5.13б). Определить нормальные
напряжения в точках
(рис. 5.13б). Определить нормальные
напряжения в точках ![]() в заделке.
в заделке.
 Решение.
Решение.
Определяем внутренние усилия: 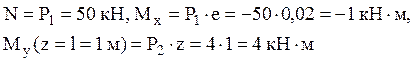 .
.
Воспользуемся формулой для вычисления
нормальных напряжений: 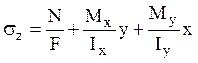
точка ![]()
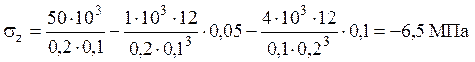 ,
,
точка ![]()
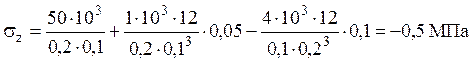 ,
,
точка ![]()
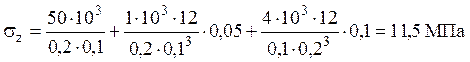 ,
,
точка ![]()
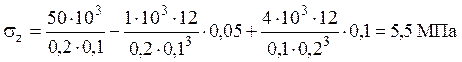 .
.
6. Кручение стержней некруглого сечения
 В общем случае при
кручении произвольного стержня поперечные сечения плоские до деформации
искривляются по некоторой поверхности
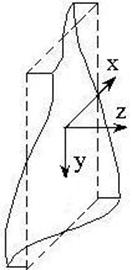
В общем случае при
кручении произвольного стержня поперечные сечения плоские до деформации
искривляются по некоторой поверхности ![]() ,
которая называется функцией депланации сечения, а само явление – депланацией.
(рис. 6.1). Значения функции депланации определяют перемещения точек сечения в
направлении оси стержня Z. Угол сдвига
,
которая называется функцией депланации сечения, а само явление – депланацией.
(рис. 6.1). Значения функции депланации определяют перемещения точек сечения в
направлении оси стержня Z. Угол сдвига ![]() образуется
как за счет наклона образующих, так и из-за наклона сторон, лежащих в
поперечных сечениях. Если депланации всех поперечных сечений одинаковы по длине
стержня, то кручение называется свободным. При этом каждое
продольное волокно перемещается в продольном направлении как жесткое целое и
нормальное напряжение в поперечных сечениях будет отсутствовать
образуется
как за счет наклона образующих, так и из-за наклона сторон, лежащих в
поперечных сечениях. Если депланации всех поперечных сечений одинаковы по длине
стержня, то кручение называется свободным. При этом каждое
продольное волокно перемещается в продольном направлении как жесткое целое и
нормальное напряжение в поперечных сечениях будет отсутствовать ![]() . Если депланации переменны по длине
стержня, то такое кручения называется стесненным, а в поперечных сечениях
наряду с касательными присутствуют и нормальные напряжения.
. Если депланации переменны по длине
стержня, то такое кручения называется стесненным, а в поперечных сечениях
наряду с касательными присутствуют и нормальные напряжения.
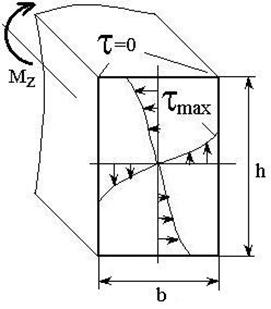
Максимальные касательные напряжения при
кручении стержня прямоугольного сечения (рис 62 возникают в средних точках
длинных сторон контура, которые равны 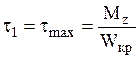 ,
,
![]() , где коэффициент
, где коэффициент ![]() зависит от соотношения высоты и
ширины прямоугольника. В серединах коротких сторон возникают меньшие
напряжения, которые равны
зависит от соотношения высоты и
ширины прямоугольника. В серединах коротких сторон возникают меньшие
напряжения, которые равны ![]() .
.
Для угловых точек касательные напряжения
равны нулю, что следует из закона парности касательных напряжений (боковая
поверхность свободна от напряжений). Угол закручивания связан с крутящим
моментом соотношением 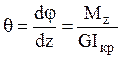 , где
, где ![]() ,
, ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.