Конспект лекционных и практических занятий по дисциплине "Сопротивление материалов", страница 6

Абсолютное значение отношения относительной поперечной деформации к относительной продольной деформации при растяжении или сжатии в области действия закона Гука называется коэффициентом Пуассона: ;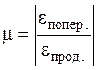

Данный коэффициент является упругой константой изотропного материала и определяется экспериментально. Коэффициент Пуассона безразмерен.

Диапазон изменения значений коэффициента Пуассона:  (на практике ).

Пример: сталь - ; резина, каучук - ; пробка, парафин - ;

Условие прочности при одноосном растяжении-сжатии:

Опасными сечениями при одноосном растяжении-сжатии являются те, где отношение продольной силы к площади поперечного сечения достигает максимума: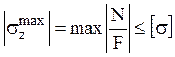

3.3 Определение осевых перемещений

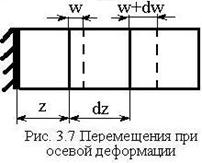Пусть два бесконечно-близких расположенных сечения стержня с координатами  и  при его осевой деформации перемещаются на расстояния  и  соответственно. Тогда

удлинение участка стержня длиной  будет , а относительная деформация 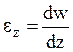. Для линейно-упругого материала используем закон Гука: 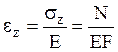 или 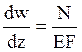 (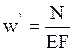), где  - жесткость стержня при осевой деформации. Выражение для продольного перемещения получим интегрированием по осевой координат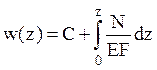е: , где  - константа интегрирования. Для . Таким образом, константа интегрирования  является перемещением в начале координат. Продольное перемещение произвольного сечения определяется выражением .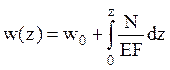

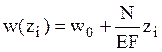Если на определенном участке , то  - перемещения меняются по линейному закону, а деформация постоянна.

Полное удлинение (укорочение) стержня постоянной жесткости  при растяжении (сжатии) постоянной силой : .

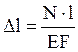Пример:

Определить перемещения под действием собственного веса, если известны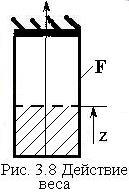 - объемный вес материала стержня (вес единицы объема); ,

где  - плотность материала,  - ускорение свободного падения,

 - площадь поперечного сечения (рис. 3.8);

Решение.

Совмещаем начало координат со свободным концом стержня,

Значение осевой силы равно весу нижележащей (заштрихованной) части стержня: .

Перемещение под действием этой силы .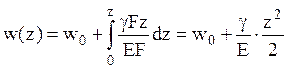

Определим перемещение свободного конца из условия равенства нулю перемещения у заделк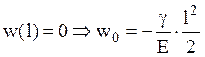и  и .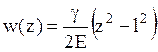

Полное удлинение стержня от собственного веса (перемещение свободного конца) равно ;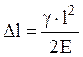

при 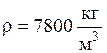,  (сталь), : 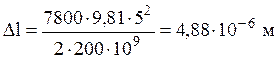. Вследствие того, что перемещения под действием собственного веса ничтожно малы, ими, как правило, в расчетах пренебрегают.

Стержень переменного сечения, у которого напряжения во всех сечениях одинаковы и близки к предельно-допустимым называется стержнем равного сопротивления растяжению или сжатию.

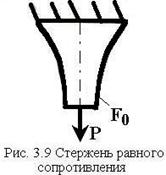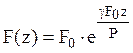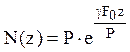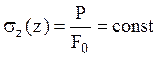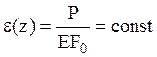Площадь поперечного сечения такого стержня (рис. 3.9) меняется по экспоненциальному закону: , также как и продольная сила , напряжения , деформации , продольные перемещения  меняются по линейному закону. На практике используются стержни, имеющие сечения, близкие к экспоненциальному: ступенчато-постоянные и конусообразные.

3.4 Статически-неопределимые системы при растяжении-сжатии

Системы, в которых число наложенных связей больше числа уравнений статического равновесия называются статически-неопределимыми

Разница между числом неизвестных и числом независимых уравнений статического равновесия называется степенью статической неопределимости.

Свойства статически-неопределимых систем

-  невозможно определить все усилия из одних только уравнений статического равновесия

-  должны быть геометрически-неизменяемыми, т.е. должна отсутствовать возможность перемещений при постоянной силе

-  для раскрытия статической неопределимости необходимо составить дополнительные условия – условия совместности деформаций (уравнения перемещений), которые означают, что до и после деформации система представляет из себя единую конструкцию.

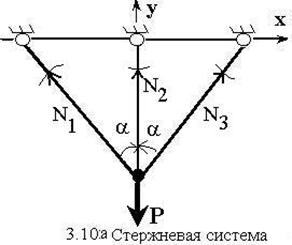Пример: три стержня соединены в шарнире (рис. 3.10а), в котором действует вертикальная сосредоточенная сила , а сверху стержни закреплены в неподвижных шарнирах. Угол между крайними стержнями и вертикалью в ненагруженном состоянии . Длина среднего стержня . Материал стержней одинаков, модуль Юнга равен . Площадь поперечного сечения крайних стержней , а среднего стержня .

Определить продольные силы, напряжения в стержнях, а также удлинение среднего стержня.

Решение.

Вводим прямоугольную систему координат, совмещая ее начало с шарниром, в котором действует сила. Рассекаем стержни в произвольной точке по их длинам – получаем три внутренних усилия: .

Составляем уравнения статического равновесия:

 (условие симметрии)

условие равенства нулю всех моментов относительно точки A:

 - является вырожденным.

Поскольку два оставшихся уравнения равновесия содержат три неизвестных, то система является статически-неопределимой. Степень статической неопределимости равна единице.

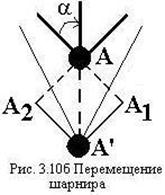
Рассматриваем совместную деформацию стержней: при действии силы  стержень 2 удлиняется, при этом стержни 1 и 3 удлиняясь, поворачиваются вокруг верхних неподвижных шарниров, оставаясь соединенными со стержнем 2.

Считая перемещения малыми, заменяем перемещения крайних стержней по дугам окружностей на перемещения по перпендикулярам к их исходному положению (рис. 3.10б). Из геометрии следует, что 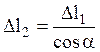. Используя закон Гука (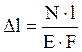), получим дополнительное третье уравнение: .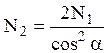

Решая полученную систему алгебраических уравнений, получим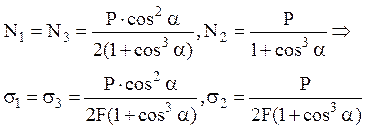

при этом удлинение среднего стержня составит 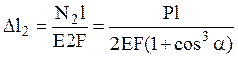. Поскольку , то  и средний стержень оказывается более напряженным.

3.5 Температурные и монтажные напряжения

Возникающие при изменении температуры в статически-неопределимых системах дополнительные усилия (напряжения) называются температурными усилиями (напряжениями).

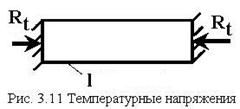Пример: для статически-неопределимого стержня постоянной жесткостью и длиной , температура которого увеличена на , определить температурные напряжения.

Решение.

Удлинение из-за действия температуры определяется как ,

где  - коэффициент температурного расширения;

это же удлинение, но по закону Гука: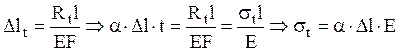

при  (сталь), : .