Конспект лекционных и практических занятий по дисциплине "Сопротивление материалов", страница 5

Радиусом инерции сечения относительно некоторой оси называется величина, определяемая по формуле: .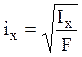

Радиусы инерции, определенные для главных осей, называются главными радиусами инерции: .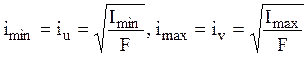

Определив главные радиусы инерции, можно построить главный эллипс инерции:

- провести главные оси

- отложить по оси  радиус ,

а по оси  радиус  по обе стороны от начала координат

- по полученным четырем точкам построить эллипс

Свойства эллипса инерции:

-  эллипс инерции ориентирован в направлении распределения материала сечения;

-  -расстояние между произвольной осью, проходящей через центр эллипса  и осью, параллельной оси  и касающейся эллипса является радиусом инерции  для данной оси, т.е.

Пример

Положения главных осей для простейших сечений

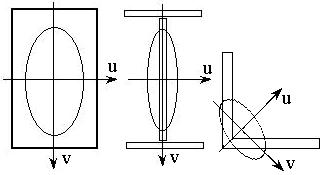
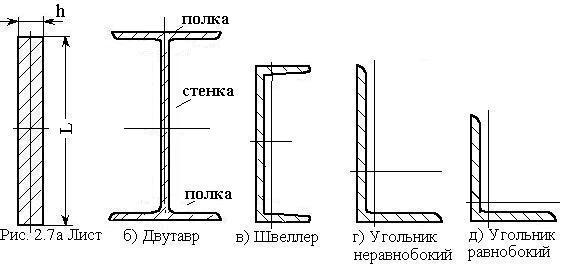Стандартные тонкостенные сечения (рис. 2.7) задаются номером (например, двутавр №20 или угольник №12.5/10.0). Геометрические характеристики стандартных тонкостенных профилей определяются по стандарту - сортаменту прокатных профилей по заданному номеру, который определяет высоту профиля или длины его сторон в [см].

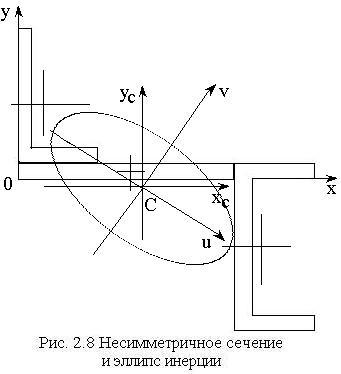2.7 Пример выполнения расчетно-графической работы № 1: Определение геометрических характеристик плоской фигуры

Для заданного несимметричного сварного профиля, состоящего из

2)  листа 200x9 мм,

3)  швеллера №16,

4)  уголка неравнобокого №14/9 (толщина стенки t=8мм)

осуществить

1)  определение положения центра тяжести

2)  определение положения главных центральных осей

3)  построение центрального эллипса инерции

Выполнение данной работы удобно проводить, заполняя следующую таблицу:

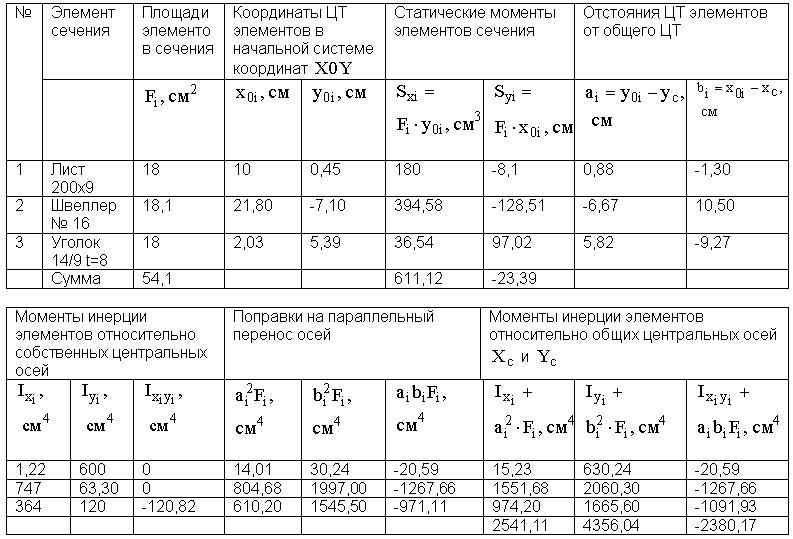
Порядок выполнения расчетно-графической работы:

1) Для заданных профилей определяем или берем из сортамента их начальные геометрические характеристики

- для листа

- для швеллера

- для уголка

2) Вводим произвольную начальную систему координат: в данном случае начало координат (точка ) совмещено с левым нижнем концом листа и изображаем в выбранном масштабе составное сечение;

в) Определяем центры тяжести отдельных элементов: исходя из схемы сечения

- для листа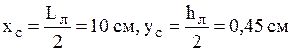

- для швеллера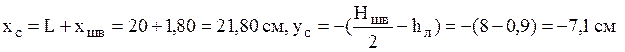

- для уголка

и заносим их реальные значения в таблицу;

3) Определяем статические моменты элементов сечения ,  и всего сечения относительно начальной системы координат ;

4) Координаты ЦТ всего сечения: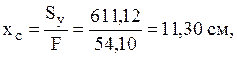  

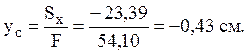
5) Изображаем на чертеже центр тяжести и центральные оси всего сечения (точка  и оси );

6) Определяем координаты центров тяжестей отдельных элементов в системе центральных осей

7) Определяем или берем из сортамента моменты инерции элементов сечения для собственных центральных осей

- для листа ;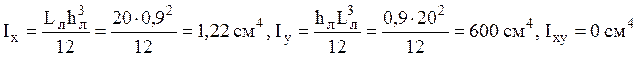

- для швеллера

- для уголка ;

Центробежный момент инерции для неравнобокого уголка  с толщиной стенки  относительно собственных центральных осей определим по формуле:

.

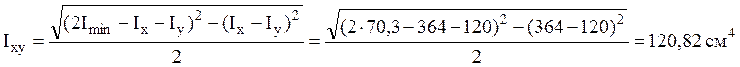В таблицу записываем , поскольку большая часть площади уголка находится в области, где координаты  и  точек сечения имеют противоположные знаки.

Осевые моменты инерции записываем в таблицу исходя из реального положения элементов относительно осей .

8) Определяем поправки на параллельный перенос при переходе от собственных центральных осей каждого элемента к общим центральным осям ;

9) Определяем моменты инерции элементов сечения и всего сечения относительно общих центральных осей ;

10) Угол, задающий положение главных центральных осей, определяется по формуле

.

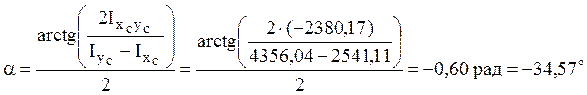Поскольку угол отрицателен, то откладываем его по часовой стрелке и проводим одну из главных осей .

11) Главные центральные моменты инерции равны

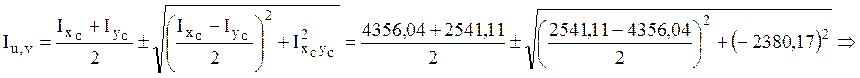
, при этом т.к. , то .

12) Главные центральные радиусы инерции равны

.

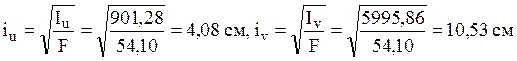Откладывая по оси  радиус , а по оси  – радиус , строим эллипс инерции.

3. Одноосное растяжение-сжатие

3.1 Напряжения и деформации при растяжении и сжатии

Принцип Сен-Венана: распределение напряжений существенно зависит от способа приложения внешних сил лишь вблизи места нагружения, а в частях достаточно удаленных от места приложения сил распределение практически зависит только от статического эквивалента этих сил. На рис. 3.1 показан пример систем, имеющих одинаковые главный вектор и главный момент, поэтому деформацию этих систем будем считать одинаковой.

Гипотеза Я Бернулли (гипотеза плоских сечений): поперечные сечения стержня плоские и перпендикулярные его продольной оси до деформации остаются плоскими и перпендикулярными к его оси и после деформации. В таком случае нормальные напряжения можно считать распределенными постоянно по сечению и формула для нормальных напряжений при одноосном растяжении-сжатии принимает вид .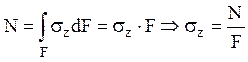

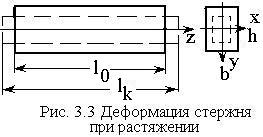
Правило знаков при осевой деформации растягивающая сила (напряжение) – положительна, сжимающая – отрицательна:

Разница между длиной стержня после деформации и начальной длиной стержня называется абсолютной продольной деформацией стержня: .

Отношение абсолютной продольной деформации к начальной длине стержня называется относительной продольной деформацией: .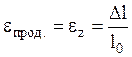

Отношение абсолютной поперечной деформации стержня к его начальному поперечному размеру называется относительной поперечной деформацией: .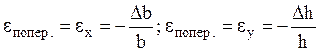

Для изотропных материалов поперечные деформации равны между собой: .

Деформации  называются также линейными деформациями потому что определяют изменение линейных размеров и являются безразмерными величинами.

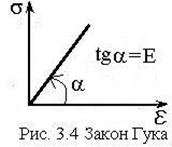
3.2 Закон Гука при одноосном растяжении

Р. Гук из экспериментов установил,  что во многих случаях деформация прямо пропорциональна вызываемому ее усилию.

Закон Гука при одноосном растяжении: при малых перемещениях, деформация и нормальное напряжение, ее вызвавшее, пропорциональны друг другу: ,

где  - модуль продольной упругости (модуль Юнга) – упругая константа изотропного материала, .

Пример: углеродистая сталь ; медь, ; дерево  (вдоль волокон),  (поперек волокон).