1) 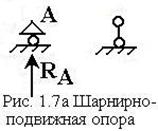 шарнирно-подвижная
опора – устройство, позволяющее перемещение опорного сечения
параллельно опорной плоскости и поворот его в вертикальной плоскости
относительно оси цилиндрического шарнира, но не дающего возможности перемещения
в направлении наложенной связи по вертикали. Реакция такой опоры направлена
вдоль опорной связи (рис. 1.7а);
шарнирно-подвижная
опора – устройство, позволяющее перемещение опорного сечения
параллельно опорной плоскости и поворот его в вертикальной плоскости
относительно оси цилиндрического шарнира, но не дающего возможности перемещения
в направлении наложенной связи по вертикали. Реакция такой опоры направлена
вдоль опорной связи (рис. 1.7а);
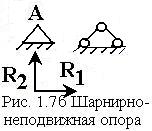 2) шарнирно-неподвижная
опора не допускает смещений опорного сечения ни в продольном, ни
в поперечном направлениях, но допускает поворот этого сечения относительно
шарнира. На данной опоре возникают две реакции, направленные по оси балки и
перпендикулярно оси балки (рис. 1.7б);
2) шарнирно-неподвижная
опора не допускает смещений опорного сечения ни в продольном, ни
в поперечном направлениях, но допускает поворот этого сечения относительно
шарнира. На данной опоре возникают две реакции, направленные по оси балки и
перпендикулярно оси балки (рис. 1.7б);
 3) жесткое закрепление
(заделка) не допускает поворота опорного сечения и перемещения его
ни в каком направлении, т.е. на такой опоре возникают три реакции –
вертикальная и горизонтальная реакции и изгибающий момент (рис. 1.7в).
3) жесткое закрепление
(заделка) не допускает поворота опорного сечения и перемещения его
ни в каком направлении, т.е. на такой опоре возникают три реакции –
вертикальная и горизонтальная реакции и изгибающий момент (рис. 1.7в).
Типы балок:
1) консоль – балка с одним жестко защемленным концом и другим свободным концом;
2) простая – однопролетная балка, имеющая по концам шарнирные опоры, расстояние между которыми называется пролетом балки;
3) консольная – простая балка, имеющая одну или две консоли.
Недопустимо соединение балки с основанием при помощи шарнирных опор, направления которых были бы параллельны друг другу или пересекались в одной точке (в противном случае конструкция будет геометрически-изменяемой). Геометрически неизменяемые системы, в которых опорные реакции и внутренние усилия могут быть найдены из одних только уравнений статического равновесия, называются статически определимыми.
В случае если число наложенных на систему связей больше числа уравнений равновесия система является статически-неопределимой.
1.8 Условие прочности и задачи, решаемые с его помощью
Условие прочности -
максимальное по абсолютной величине действующее в конструкции напряжение не
должно превышать определенного заданного значения: ![]() , где
, где
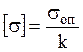 - допускаемое
напряжение (задается при расчете конструкции),
- допускаемое
напряжение (задается при расчете конструкции),
![]() -опасные
для данного материала напряжения (определяются
экспериментально),
-опасные
для данного материала напряжения (определяются
экспериментально),
![]() - коэффициент запаса
прочности;
- коэффициент запаса
прочности;
Выбор коэффициента запаса прочности определяется
- учетом конкретных условий работы конструкции;
- соответствием механических свойств материала конструкции и испытанных образцов;
- неточностью задания внешней нагрузки;
- долговечностью проектируемой конструкции;
Задачи, решаемые с помощью условия прочности:
а) проверка прочности: заданы все размеры конструкции и вся нагрузка. Необходимо проверить выполняется ли условие прочности;
б) определение минимально-необходимых размеров: заданы основные размеры конструкции и вся нагрузка. Необходимо определить недостающие минимально-необходимые размеры, исходя из выполнения условия прочности;
в) определение грузоподъемности: заданы все размеры конструкции и основная нагрузка. Необходимо определить максимальное значение (грузоподъемность) какой-то нагрузки, исходя из выполнения условия прочности;
1.9 Примеры построения эпюр внутренних усилий
а) статически-определимая плоская рама
Построить эпюры ![]() для рамы, показанной на рис. 1.8а
для рамы, показанной на рис. 1.8а
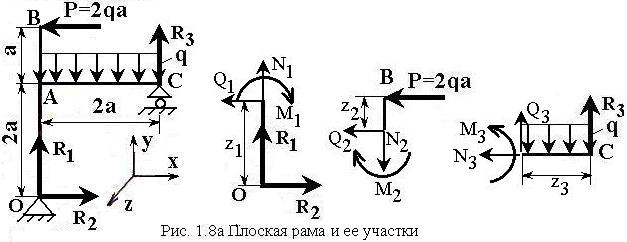
При построение продольную силу считать положительной, если она осуществляет растяжение стержня. Поперечную силу положительной, если она осуществляет поворот элемента стержня по часовой стрелке. Изгибающий момент откладывать со стороны сжатых волокон стержня.
Решение.
Отбрасывая шарнирные опоры, заменяем их действие на действие соответствующих реакций. Для их определения составляем уравнения статического равновесия:
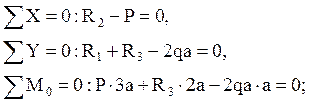
Отсюда
при ![]() :
: ![]()
Разделяем раму на три участка OA, AB, AC и рассекаем каждый из них в произвольной точке. Составляя уравнения равновесия оставшейся части каждого из участков, определяем внутренние усилия (рис. 1.8а):
На участке OA, рассматривая равновесие нижней части стержня, имеем
![]() (сжаты правые волокна
стержня OA).
(сжаты правые волокна
стержня OA).
На участке AB, рассматривая равновесие верхней части стержня, имеем
![]() (сжаты левые волокна
стержня AB).
(сжаты левые волокна
стержня AB).
На участке AС, рассматривая равновесие правой части стержня, имеем
![]() (сжаты
нижние волокна стержня AC).
(сжаты
нижние волокна стержня AC).
По полученным аналитическим выражениям строим эпюры продольных, поперечных сил и изгибающих моментов (рис 1.8б)
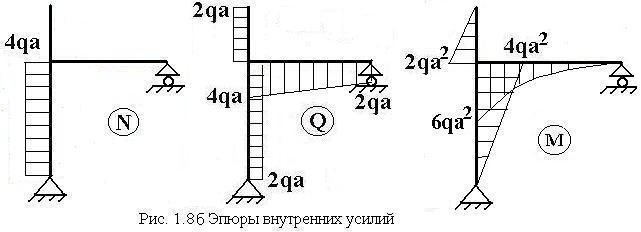
Правильность построения эпюр можно проверить с использованием
1) дифференциальных соотношений между внутренними усилиями при изгибе;
2) составления уравнений статического равновесия произвольного участка, вырезанного из рамы;
3) проверки соблюдения граничных условий.
б) криволинейный стержень
Построить
эпюры ![]() для
криволинейного стержня (см. рис. 1.9a)
для
криволинейного стержня (см. рис. 1.9a)
Для
построения эпюр необходимо определить только реакцию ![]() . Составляем условие равенства нулю
суммы всех моментов относительно точки A:
. Составляем условие равенства нулю
суммы всех моментов относительно точки A:
![]()
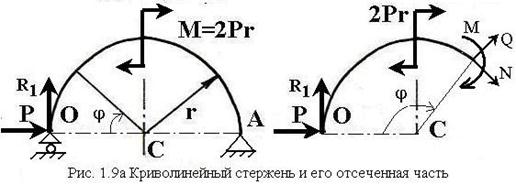
Рассекаем
стержень под произвольным углом ![]() (рис.1.9а), отбрасываем
левую часть и определяем внутренние усилия из уравнений равновесия в проекциях
на нормальное и касательное направления к оси стержня в каждой точке:
(рис.1.9а), отбрасываем
левую часть и определяем внутренние усилия из уравнений равновесия в проекциях
на нормальное и касательное направления к оси стержня в каждой точке:
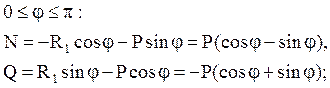
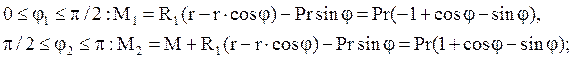
Для построения эпюр определяем значения внутренних усилий для разных значений углов:
при ![]()
![]()
при ![]() (чуть левее середины стержня)
(чуть левее середины стержня)
при ![]() (чуть правее середины стержня)
(чуть правее середины стержня)
![]()
при ![]()
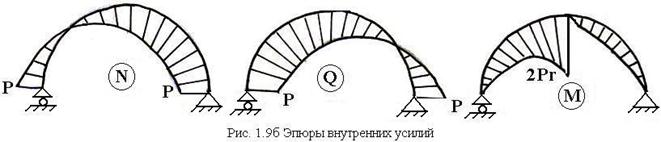
Откладывая полученные значения по перпендикулярно оси стержня (по его радиусу), строим эпюры внутренних усилий (рис. 1.9в)
2. Геометрические характеристики плоских сечений
2.1 Статические моменты и центр тяжести
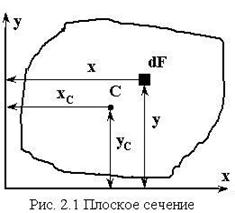
Рассмотрим плоское сечение и введем
прямоугольную декартову систему координат. Для того, чтобы охарактеризовать
площадь поперечного сечения введем характеристику 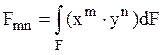 .
Тогда характеристика нулевого порядка является площадью
поперечного сечения и равна
.
Тогда характеристика нулевого порядка является площадью
поперечного сечения и равна 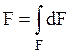 (для
(для ![]() ).
).
![]() Статическим моментом
сечения площади
Статическим моментом
сечения площади ![]() относительно данной оси
называется сумма произведений элементарных площадей
относительно данной оси
называется сумма произведений элементарных площадей ![]() на
их расстояния до данной оси, определенная для всей площади
на
их расстояния до данной оси, определенная для всей площади ![]()
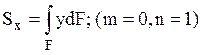 ,
, 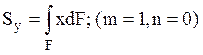 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.