Конспект лекционных и практических занятий по дисциплине "Сопротивление материалов", страница 4

Размерность статических моментов  (). Значение статического момента может быть отрицательным, положительным и равным нулю. Ось, относительно которой статический момент равен нулю, называется центральной. Точка пересечения центральных осей называется центром тяжести (в этой точке приложена равнодействующая сил тяжести). В случае если положение центра тяжести известно, то статический момент относительно произвольной оси равен произведению всей площади  на расстояние от этой оси до центра тяжести данного сечения.

, .

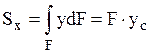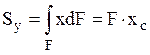Центр тяжести произвольного сечения определяется по формулам

, .

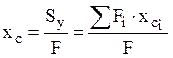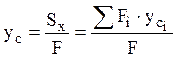Суммирование производится по всем простейшим составным частям сечения , при этом отсутствующие части сечения (например, вырез или дополнения до целого) берутся отрицательными.

Если сечение имеет хотя бы одну ось симметрии, то центр тяжести лежит на данной оси.

Центр тяжести для прямоугольника находится на пересечении его диагоналей, для круга – в его центре, для прямоугольного треугольника – на расстоянии равном 2/3 длины его катетов от каждой из его вершин, образующих острые углы.

Пример.

Для симметричного сечения, состоящего из квадрата со стороной a=10см и круга с диаметром D=10см, определить положение центра тяжести  (рис. 2.2).

Решение:

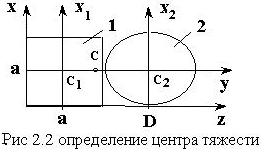Вводим прямоугольную систему координат , проходящую через центры тяжести отдельных элементов.

Тогда в силу симметрии

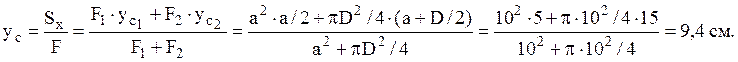
Поскольку квадрат со стороной равной диаметру круга имеет большую площадь, то центр тяжести всего сечения, лежащий на оси , оказывается ближе к центру тяжести квадрата.

2.2 Моменты инерции и моменты сопротивления сечения

Осевым моментом инерции сечения  относительно данной оси  называется сумма произведений элементарных площадей  на квадрат расстояний до данной оси, определенная для всей площади : 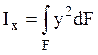; по аналогии для оси : 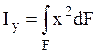. Они являются характеристиками плоского сечения второго порядка для  и  соответственно.

Полярным моментом инерции сечения  относительно данной точки (полюса) называется сумма произведений элементарных площадей  на квадрат расстояний до данной точки, определенная по всей площади : .

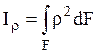Размерность осевых и полярного моментов инерции . Их значения могут быть только положительными. Сумма осевых моментов инерции относительно пары двух любых взаимно перпендикулярных осей  и , проходящих через данную точку, постоянна и равна полярному моменту инерции относительно центра координат: .

Центробежным моментом инерции  относительно двух осей  и  называется сумма произведений элементарных площадей  на расстояния до двух этих осей, определенная для всей площади : 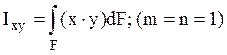. Его значение может быть отрицательным, положительным и равным нулю.

Осевые моменты инерции для простейших сечений:

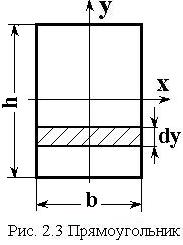а) определить осевые моменты инерции для прямоугольника с шириной  и высотой .

Решение:

Разбивая сечение на бесконечно-тонкие прямоугольники (рис. 2.3) и интегрируя по высоте сечения, получим ,

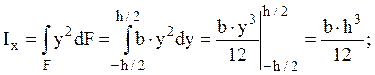 по аналогии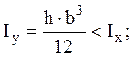

б) определить осевые моменты инерции для круга диаметром D.

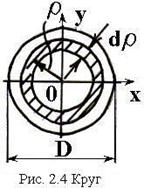Пользуясь тем, что для круга , определим :

Разбивая сечение на бесконечно-тонкие кольца (рис. 2.4) и интегрируя от центра круга до наружного радиуса, получим ,

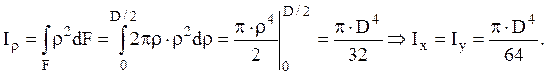
Моментом сопротивления относительно данной оси  называется отношение осевого момента инерции для данной оси к максимальному расстоянию  точек сечения от данной оси, взятому по модулю: .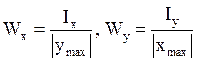

2.3 Определение статических моментов и моментов инерции при параллельном переносе осей

Пусть  – центральные оси. Определить ,

если   известны.

Решение.

Связь между новыми и старыми координатами: , используем определения моментов:

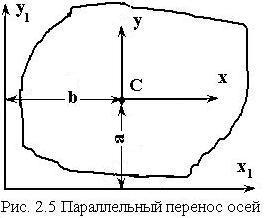
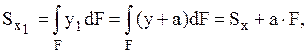
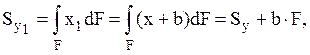
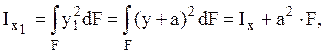
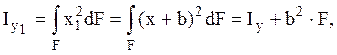
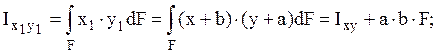
Таким образом, для того чтобы определить новые значения моментов необходимо добавить к их старым значениям поправку на параллельный перенос равную произведению площади поперечного сечения на расстояние между осями в степени соответствующей порядку характеристики (значений ).

Поскольку поправки, определяющие пересчет осевых моментов инерции, всегда положительны, то их значения для центральных осей минимальны.

2.4 Определение моментов инерции при повороте осей

Пусть  – произвольные оси и угол >0 – по часовой стрелке. Определить , если  известны.

Решение.

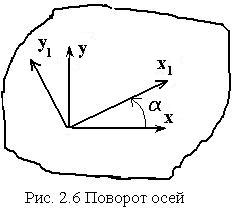Связь между координатами: , используем определения моментов инерции:

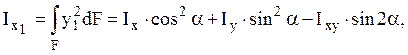
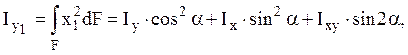
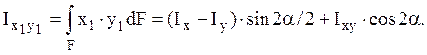
Пример.

Для составного сечения (рис.2.2) определить осевые и центробежный моменты инерции и моменты сопротивления .

Решение:

Пользуясь формулами для определения моментов инерции при параллельном переносе осей, суммируя моменты инерции для отдельных элементов сечения, получим

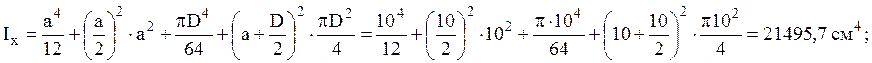
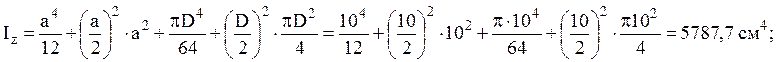
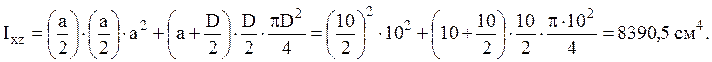
Максимальным расстоянием от оси  является (), а от оси  является , поэтому

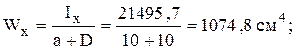
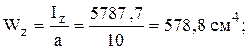
2.5 Главные оси и главные моменты инерции.

Оси, относительно которых центробежный момент инерции равен нулю, называются главными. Положение таких осей можно найти в каждой точке плоского сечения. Если начало координат этих осей совпадает с центром тяжести, то такие оси называются главными центральными. Моменты инерции относительно главных центральных осей называются главными (главными центральными) моментами инерции. Формулу для определения положения главных осей инерции по отношению к произвольным осям получим из условия отсутствия центробежного момента инерции, возникающего при повороте осей: .

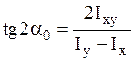Подставив найденное значение угла в выражения для осевых моментов инерции при повороте осей, получим формулу для определения главных моментов инерции: .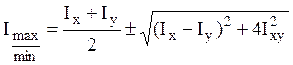

Главные моменты инерции обладают свойством экстремальности – один из них имеет наибольшее, а другой – наименьшее значение из всех моментов инерции для любой оси, проходящей через данную точку.

Знак ‘+’ берется для наибольшего момента инерции, а знак ‘-’ для наименьшего.

Главные центральные оси инерции обозначаются часто буквами  и , а главные моменты инерции  и  соответственно.

2.6 Радиусы и эллипс инерции