Требования морских потребителей к точности местоопределения судов по регламенту Международной Морской Организации, страница 6

Основными качественными показателями устройств поиска приемоиндикаторов РНС являются вероятность правильного окончания поиска  и среднее время поиска . Значения этих параметров определяются вероятностями ошибок первого и второго рода (ложной тревоги  и пропуска сигнала ), а также временем анализа  на каждом шаге поиска (которое, в свою очередь, также определяет вероятности ошибок  и ).

В общем случае вывод формул, связывающих показатели  и   с указанными параметрами, достаточно сложен. Однако для случая, когда выполняется условие  (представляющего наибольший практический интерес), формулы для   и   при последовательном поиске принимают вид

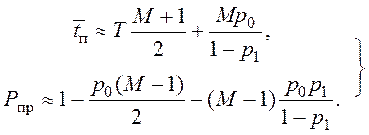                                                 (24)

Как свидетельствуют результаты расчетов по формулам (24), при  и , значение вероятности пропуска , минимизирующее время поиска, составляет 0,05–0,1 .

Значения вероятностей ошибок  и  определяются алгоритмом обнаружения сигнала, используемым в устройстве поиска.

В соответствии с результатами теории обнаружения сигналов оптимальный алгоритм обнаружения сигнала сводится к формированию на интервале наблюдения [0,Т] отношения правдоподобия (или монотонной функции от него, например ln(x)) и сравнению его с порогом. Причем структура устройства, реализующего оптимальный алгоритм (структура оптимального обнаружителя) не зависит от выбранного критерия оптимальности (выбор критерия сказывается лишь на величине порога обнаружения, который при использовании наиболее распространенного критерия Неймана – Пирсона выбирается из условия обеспечения заданной вероятности  ложной тревоги).

Применительно к задаче поиска сигнала по задержке, когда начальная фаза сигнала не известна, оптимальный алгоритм обнаружения сигнала можно представить в виде

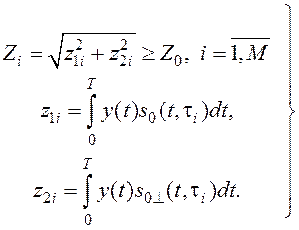                                                                   (25)

Здесь и  – корреляции принятой реализации y(t) смеси сигнала и шума (или только шума) с опорными сигналами  и , являющимися квадратурными копиями сигнала  при значении параметра ;  – порог обнаружения, выбираемый по заданной вероятности .

Структурная схема оптимального корреляционного обнаружителя с квадратурными каналами, реализующего алгоритм (25), представлена на рис. 29, где ПР – преобразователь, осуществляющий операцию формирования величин Z_i (25); ПУ – пороговое устройство.

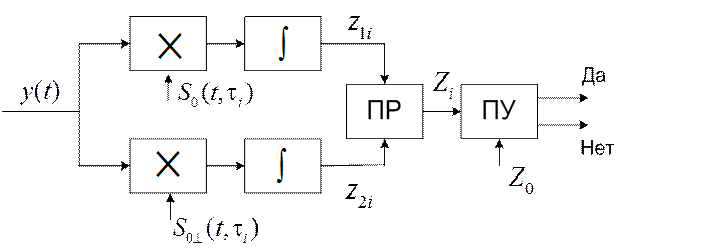       Рис. 29. Структурная схема оптимального корреляционного обнаружителя сигнала с неизвестной фазой

При обнаружении импульсных сигналов (импульсно-фазовые РНС) предпочтительнее другой вариант реализации оптимального обнаружителя –  на основе согласованного фильтра (СФ). Вычисление квадратурных компонент   и  (рис. 30) осуществляется в этом случае путем стробирования во временных селекторах (ВрС) выходного напряжения СФ в моменты  и  ( – период высокочастотного заполнения сигнальных импульсов) с последующим накоплением полученных отсчетов за время  ( –  период повторения сигнальных импульсов).

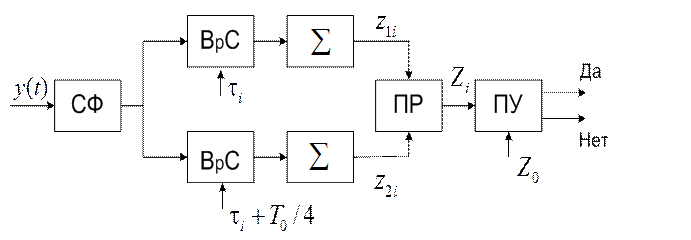
Рис. 30. Структурная схема оптимального обнаружителя (на основе СФ) сигнала

 с неизвестной фазой

При обнаружении многочастотного сигнала (фазовые РНС) оптимальный алгоритм принятия решения имеет вид

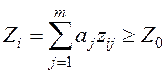                                       .                                                (26)

В соответствии с уравнением (26) решение о наличии или отсутствии сигнала принимается на основе сравнения с порогом величины , полученной путем накопления величин по всем   частотным посылкам с весами (), определяемыми уровнем сигнала данной частоты. Формирование величин    по каждой частотной посылке осуществляется в соответствии с алгоритмом (25).

Трудности, связанные с определением неизвестных весовых коэффициентов (амплитуд посылок), можно преодолеть, отказавшись от весовой обработки (полагая  для всех j). Потери при равновесной обработке по сравнению с оптимальной (весовой) обработкой многочастотного сигнала не превышают 25 %, если число частотных посылок   10.