Требования морских потребителей к точности местоопределения судов по регламенту Международной Морской Организации, страница 15

Здесь  – параметр, определяющий добротность системы по ускорению – коэффициент передачи дискриминатора; 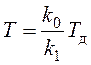 – постоянная времени, определяющая коэффициент передачи в интегрирующей ветви сглаживающего фильтра (рис. 54); 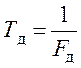 – период дискретизации сигнала ошибки.

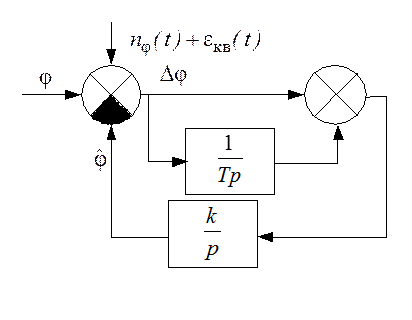
Рис. 54.  Линейная непрерывная модель цифрового следящего

измерителя фазы

С помощью уравнения (132) определяется передаточная функция замкнутой системы

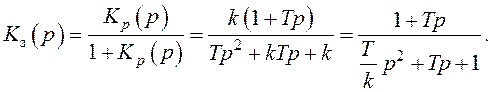                     (133)

Как видно из (133), передаточная функция  определяется двумя параметрами  и Т, полностью характеризующими качественные показатели следящего измерителя (точность, запас устойчивости, быстродействие, перерегулирование и пр.).

Рассматриваемая система является устойчивой при любых значениях параметров  и Т (постоянная времени Т всегда больше нуля). В этом случае имеет смысл говорить лишь о запасе устойчивости по фазе, который определяется значением фазочастотной характеристики (ФЧХ) форсирующего звена. Его передаточная функция определяется множителем (1+Тр) в числителе (132):

                                        (134)

Для определения частоты среза можно построить логарифмическую АЧХ (асимптотическую ЛАХ разомкнутой системы, рис. 55.

Используя асимптотическое представление ЛАХ на участке частот

                           (135)

и приравняв (135) к нулю, находятя частоту среза . После подстановки этого значения в (134) получается

                                           (136)

Качество переходных процессов в системе определяется, главным образом, параметрами колебательного звена, передаточная функция которого соответствует знаменателю выражения (133): частотой собственных колебаний 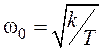 и коэффициентом затухания 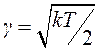. Для приемлемого качества переходного процесса необходимо выбирать g = 0,5–1, что соответствует значениям kT = 1–4. При kT > 4 () переходной процесс в системе носит апериодический характер, при kT < 4 () – колебательный.

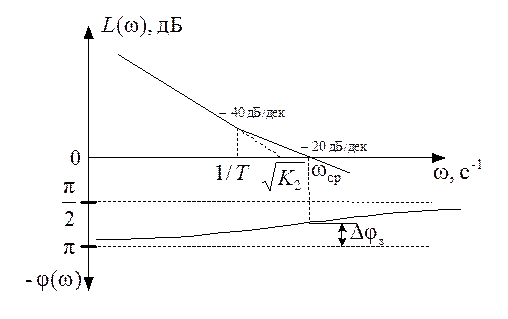
Рис. 55. ЛАХ и ЛФХ разомкнутой системы

Величина перерегулирования при этом не превышает 30 %, а длительность переходного процесса .

Дисперсия шумовой составляющей фазовой ошибки в соответствии с (101) определяется как

                                                    (137)

где  – спектральная плотность эквивалентных фазовых флуктуаций ;  – спектральная плотность шума на выходе дискриминатора эквивалентной непрерывной системы (рис. 54).

Для определения параметров дискриминационной (крутизны ) и флуктуационной (спектральной плотности ) характеристик дискриминатора можно воспользоваться формулой (57) (применительно к ФД с треугольной характеристикой, аппроксимирующей характеристику цифрового ФД при многоуровневом квантовании фазовой ошибки (при )). Тогда в соответствии с уравнением (116) для среднего значения  сигнала ошибки (128) (случай слабого сигнала, когда ) можем записать

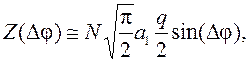                                     (138)

где  – коэффициент, определяемый формой характеристики ФД (треугольной).

Дисперсия сигнала ошибки с учетом предположения о слабом сигнале () может быть найдена как

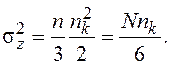                                            (139)

Здесь – числовой эквивалент интервала корреляции принятой реализации (значение , выраженное в числе счетных импульсов);  множитель n/3 определяет дисперсию каждого из  независимых отсчетов, а множитель 1/2 учитывает уменьшение дисперсии в два раза, обусловленное усреднением сигнала ошибки (128).

Как видно из уравнения (138), ДХ при  описывается гармонической функцией (с учетом предположения о большом числе уровней квантования) с пиковым значением Z_max (рис. 56), хотя в отсутствие шума (при ) ДХ аппроксимируется треугольной функцией. В этом случае коэффициент передачи дискриминатора максимален и равен   рад ^-1.

В случае слабого сигнала крутизна ДХ ,

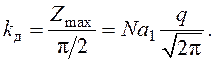                                              (140)

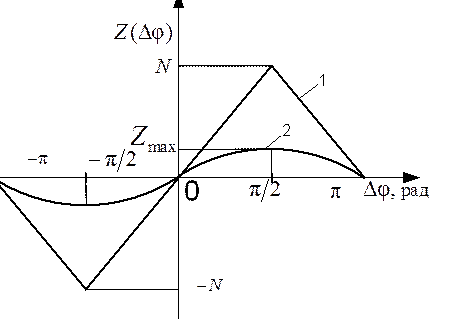
Рис. 56. Дискриминационные характеристики: 1 – при , 2 – при