Требования морских потребителей к точности местоопределения судов по регламенту Международной Морской Организации, страница 16

Полагая фазовый дискриминатор безынерционным по сравнению со сглаживающим фильтром и используя (139) для спектральной плотности  можно записать

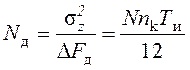                                             (141)

(эквивалентная полоса пропускания дискриминатора ).

Энергетический спектр эквивалентного фазового шума с учётом выражений (140), (141) определяется как

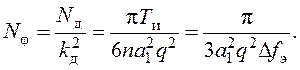                                (142)

Здесь учтено, что число независимых отсчётов  ( –  как и ранее, эквивалентная полоса линейного тракта приёмника).

Подставив (142) в (137) , для дисперсии фазовой ошибки запишется

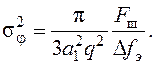                                        (143)

Определение шумовой полосы  рассматриваемой следящей системы производится с использованием табличного интеграла (104), который после подстановки в него выражения для квадрата АЧХ замкнутой системы принимает вид

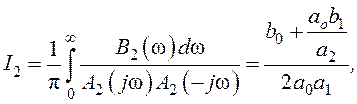                              (144)

где полиномы

После подстановки коэффициентов полиномов , , ,   и    в выражение (144) можно найти

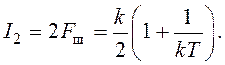                                  (145)

Выбор шумовой полосы следует производить с учётом обеспечения требуемой точности в соответствии с критерием (109). Динамическая ошибка системы второго порядка астатизма (установившееся значение) определяется как

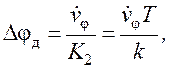                                            (146)

где  – значение второй производной процесса  (ускорение в рад ¤c²).

С целью оптимизации следящей системы по параметру kТ (146) представляется в виде

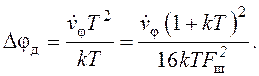                                  (147)

Минимум ошибки (147) при фиксированной полосе  (а следовательно, дисперсии шумовой ошибки) достигается при kТ = 1:

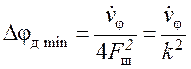.                                       (148)

Здесь учтено, что при kТ = 1 шумовая полоса).

Учитывая, что при kТ = 1 обеспечиваются приемлемые значения запаса устойчивости  и перерегулирования (около 30 %), можно рекомендовать это значение в качестве оптимального при выборе параметров системы.

Используя полученные результаты, оцениваются качественные показатели рассматриваемого следящего измерителя фазы.

Задавшись допустимой динамической ошибкой ½½< 10 ⁻³ рад при максимальном ускорении  рад ¤ с² (при длине волны  = 30 м соответствует ускорению объекта 5 м ¤ с²), из (148) можно найти

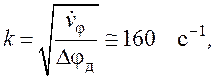
что соответствует шумовой полосе = 80 Гц.

Учитывая, что параметр k, а следовательно, и шумовая полоса , зависят от отношения сигнал/шум q (через коэффициент передачи  дискриминатора), определяется значение , соответствующее пороговому значению q_min, которое полагается равным 0,1.

Тогда в соответствии с уравнением (140) определяется

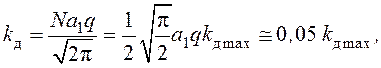
где  рад ⁻¹ – максимальное   значение   параметра   при q ® ¥ (при = 8 МГц и = 2 мс).

При фиксированных значениях параметров  и , входящих в выражение для коэффициента передачи , уменьшение отношения сигнал ¤ шум до порогового значения q_min = 0,1 приведет к уменьшению приблизительно   в   20 раз  параметра   k  и  шумовой      полосы  (соответственно k » 8 с⁻¹ и » 4 Гц). При этом динамическая ошибка возрастет в  (приблизительно в 4,5 раза) и составит рад  0,25 град (что сопоставимо с ошибкой квантования).

2 Постоянная времени Т выбирается как

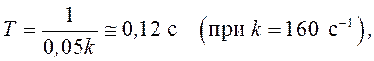
что обеспечивает приемлемое качество переходного процесса:  при q = 0,1 процесс колебательный с перерегулированием около 30 % и быстродействием

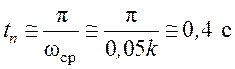, а при  он апериодический с быстродействием

По заданному значению  с и периоду дискретизации , определяется . Значения самих параметров (коэффициентов передачи k₀ прямой и интегрирующей        ветвей цифрового сглаживающего фильтра) определяются с использованием соотношения

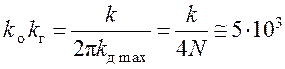 Гц

(при заданном значении коэффициента передачи ). 

В заключение оценивается дисперсия фазовой ошибки слежения при

q = 0,1 и = 4 Гц. Полагая эквивалентную полосу пропускания линейного тракта приемника =10 кГц,  в соответствии с уравнением (143) можно найти

   и СКО   град, что соответствует ошибке измерения разности расстояний (на основной масштабной частоте  = 10 МГц) ,  » 0,8 м (при равноточных измерениях фазовых сдвигов на основной и дополнительной частотах).