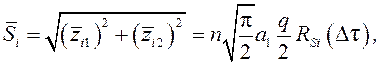 i= 1, 2.
i= 1, 2.
Отсюда можно найти среднее значение «сигнала ошибки» (111)
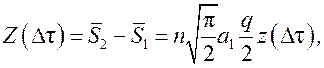
![]() , где
, где ![]() –
нормированная ДХ цифрового временного дискриминатора при многоуровневом
квантовании (треугольная характеристика).
–
нормированная ДХ цифрового временного дискриминатора при многоуровневом
квантовании (треугольная характеристика).
Дисперсия
«сигнала ошибки» с учетом предположения о слабом сигнале (![]() ) определяется как
) определяется как
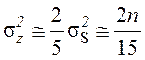 , (117)
, (117)
где 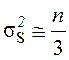 (дисперсия
каждого из n независимых отсчетов при фазовом
методе обработки равна 1/3); множитель 2/5 обусловлен тем, что сигнал ошибки (111)
формируется путем усреднения по пяти частотным посылкам разностей (S2
– S1).
(дисперсия
каждого из n независимых отсчетов при фазовом
методе обработки равна 1/3); множитель 2/5 обусловлен тем, что сигнал ошибки (111)
формируется путем усреднения по пяти частотным посылкам разностей (S2
– S1).
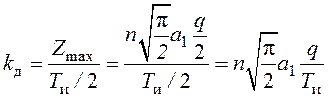 .
(118)
.
(118)
В отсутствие
шума (![]() ) коэффициент передачи ВД
максимален
) коэффициент передачи ВД
максимален
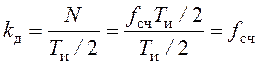
и численно равен значению частоты
![]() в МГц (изменение цифрового сигнала ошибки
на единицу соответствует изменению задержки на
в МГц (изменение цифрового сигнала ошибки
на единицу соответствует изменению задержки на ![]() микросекунд).
микросекунд).
Полагая дискриминатор безынерционным по сравнению с цифровым сглаживающим фильтром, для спектральной плотности «шума» на выходе дискриминатора можно записать
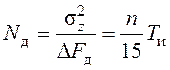 . (119)
. (119)
Здесь ![]() – эквивалентная полоса пропускания
дискриминатора, дисперсия
– эквивалентная полоса пропускания
дискриминатора, дисперсия ![]() определяется выражением
(117).
определяется выражением
(117).
Используя (118), (119), определяют энергетический спектр эквивалентных временных флуктуаций
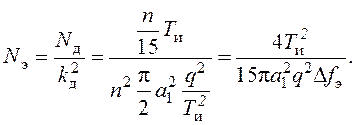 (120)
(120)
В формуле (120)
учтено, что ![]() .
.
В соответствии с уравнением (101) дисперсия шумовой составляющей ошибки слежения равна
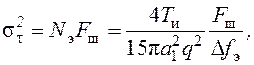 (121)
(121)
где ![]() –
шумовая полоса эквивалентной непрерывной системы.
–
шумовая полоса эквивалентной непрерывной системы.
При дискретном интегрировании операция вычисления корреляций осуществляется при этом в соответствии с правилом
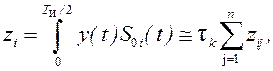 i = 1, 2, где
i = 1, 2, где ![]() –
опорный сигнал в синусном (i = 1) и косинусном (i = 2) квадратурных каналах;
–
опорный сигнал в синусном (i = 1) и косинусном (i = 2) квадратурных каналах; ![]() –
интервал корреляции процесса
–
интервал корреляции процесса ![]() (интервал
дискретизации);
(интервал
дискретизации); ![]() – независимые отсчеты на выходе
ФД (корреляции за интервал
– независимые отсчеты на выходе
ФД (корреляции за интервал ![]() ). Поэтому в формулы (116),
(118) необходимо внести изменения: умножить число n
независимых отсчетов на
). Поэтому в формулы (116),
(118) необходимо внести изменения: умножить число n
независимых отсчетов на ![]() , определяющее
длительность интервала
, определяющее
длительность интервала ![]() , выраженную в числе счетных
импульсов.
, выраженную в числе счетных
импульсов.
При этом
дисперсия сигнала ошибки (117), а, следовательно, и спектральная плотность (119)
возрастут в ![]() раз, а спектральная плотность эквивалентных
флуктуаций (120) и дисперсия ошибки (121) не изменятся.
раз, а спектральная плотность эквивалентных
флуктуаций (120) и дисперсия ошибки (121) не изменятся.
Для определения шумовой полосы следящей системы можно записать передаточную функцию замкнутой системы (рис. 50)
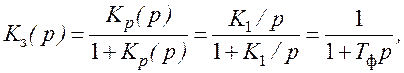 (122)
(122)
где ![]() –
добротность системы по скорости,
–
добротность системы по скорости, ![]() =1/K1 – постоянная времени эквивалентного
инерционного звена.
=1/K1 – постоянная времени эквивалентного
инерционного звена.
Как видно из (122),
показатели качества рассматриваемой системы полностью определяются параметром ![]() . Система абсолютно устойчива (при любых
значениях
. Система абсолютно устойчива (при любых
значениях ![]() ), поскольку эквивалентна фильтру нижних
частот. Переходной процесс в системе апериодический (без перерегулирования).
Время переходного процесса (быстродействие) определяется как
), поскольку эквивалентна фильтру нижних
частот. Переходной процесс в системе апериодический (без перерегулирования).
Время переходного процесса (быстродействие) определяется как ![]() .
.
Шумовая полоса системы в соответствии с (103) равна
![]()
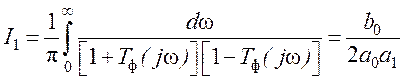 , (123)
, (123)
где ![]() –
табличный интеграл (104). Входящие в него полиномы определяются как
–
табличный интеграл (104). Входящие в него полиномы определяются как
![]()
![]() .
.
После
подстановки коэффициентов ![]() ,
, ![]() и
и ![]() в
(123), можно найти
в
(123), можно найти
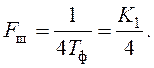 (124)
(124)
Выбор шумовой полосы должен производиться с учетом обеспечения требуемой точности слежения и приемлемого времени установления синхронизации.
Динамическая ошибка системы первого порядка астатизма (установившееся значение) определяется как
![]() ,
(125)
,
(125)
где ![]() –
скорость изменения параметра
–
скорость изменения параметра ![]() .
.
Используя (121), (125), можно определить точность рассматриваемой цифровой системы синхронизации при значениях параметров:
· дискрет
квантования задержки ![]() = 3 мкс;
= 3 мкс;
· частота счетных импульсов fсч = 8 МГц;
· интервал
измерения ![]() = 1 мс;
= 1 мс;
· длительность
цикла ![]() = 0,125 с;
= 0,125 с;
· скорость
![]() (соответствует скорости подвижного объекта
(соответствует скорости подвижного объекта
![]() ).
).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.