






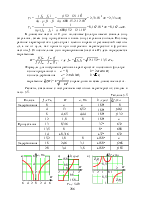











J(j1000) = 0,05·е –j100° А, J(j10000) = 0,05·е j100° А,
U2(0) = 71,43 В, U2(j100) = 70,54·е j28,61° В,
U2(j1000) = 20,96·е j136,98° В, U2(j10000) = 0,25·е -j74,27° В.
Мгновенные значения выходного напряжения:
u2(t) = 71,43 В, u2(t) = 70,54·sin(100t + 28,61°) В,
u2(t) = 20,96·sin(1000t + 136,98°) В, u2(t) = 0,25·sin(10000t – 74,27°) В.
Обращаем внимание на то, как стремительно убывают амплитуды напряжения u2 с ростом частоты, начиная с 500 рад/с. Здесь проявляются фильтрующие свойства рассматриваемого четырёхполюсника.
5.2. частотные электрические фильтры
5.2.1. Основные теоретические положения
Электрическими фильтрами (ЭФ) называют четырёхполюсники, которые пропускают к приёмнику сигналы определённого диапазона частот.
Принцип работы ЭФ базируется на зависимости от
частоты сопротивлений индуктивных и ёмкостных элементов: xL= wL, xC=![]() , а любой фильтр должен содержать хотя бы один реактивный
элемент. В идеале, ЭФ состоит только из реактивных
элементов. В этом случае он называется фильтром без потерь.
, а любой фильтр должен содержать хотя бы один реактивный
элемент. В идеале, ЭФ состоит только из реактивных
элементов. В этом случае он называется фильтром без потерь.
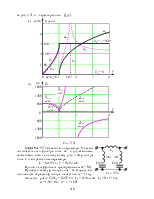
Простейшими конструктивными схемами фильтров являются симмет-ричные Т-схемы (рис. 5.42,а) и П-схемы (рис. 5.42,б), у которых продольные параметры заданы как продольное сопротивление Z1 или ½Z1, а поперечные – определяются через проводимости Y2 = Z2-1 или ½Y2, что позволяет для обеих схем определить постоянную передачи по одной формуле:
chГ= ch(a + jb) = 1
+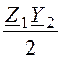 , а характеристические сопротивления следующим образом:
, а характеристические сопротивления следующим образом:
ZCT=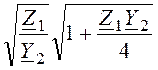 , ZCП=
, ZCП=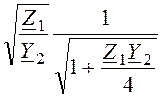 .
.
 |
Основными характеристиками фильтров являются частотные характеристики a(w), b(w), ZC(w), если для анализа используются уравнения четырёхполюсника с характеристическими параметрами, или H(w), j(w), если для анализа используются передаточные функции.
Заметим, что для идеальных фильтров (фильтров без потерь) областью пропускаемых частот (зоной прозрачности) называют диапазон частот, для которого коэффициент затухания a = 0.
По соотношению параметров различают реактивные фильтры типа k, для которых Z1×Z2 = k 2 – вещественное число, и фильтры типа m, которые являются производными (определённым образом преобразованные) от фильтров типа k.
5.2.2. Фильтры типа k
Коэффициент k = r =![]() носит название «номинальное характерис-тическое сопротивление» или «параметр
нагрузки». Формулы для расчёта основных характеристик фильтров НЧ и ВЧ
типа k приведены в табл. 5.4. Здесь x= w/w0
– относительная частота.
носит название «номинальное характерис-тическое сопротивление» или «параметр
нагрузки». Формулы для расчёта основных характеристик фильтров НЧ и ВЧ
типа k приведены в табл. 5.4. Здесь x= w/w0
– относительная частота.
Таблица 5.4
Параметры |
ФНЧ |
ФВЧ |
|
Частота среза |
w0 = |
w0 = |
|
Постоянная передачи Г= a + jb |
chГ= 1 – 2x 2 |
chГ= 1 – |
|
Коэффициент затухания |
a = 0; cha = 2x 2– 1 |
cha = a = 0 |
|
Коэффициент фазы |
cosb= 1 – 2x 2; b = +p |
b = -p; cosb= 1 – |
|
Характеристическое сопротивление |
ZCТ = r × ZCП = |
ZCТ = r × ZCП = |
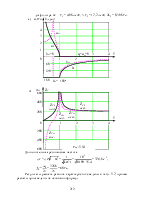
Полосовые (ПФ) и заграждающие (ЗФ) фильтры предназначены для про-пускания (или подавления) одной или нескольких узких полос частот w 1 ÷ w 2 сигнала. Полосовые фильтры формируют из каскадно соединённых низкочас-тотного и высокочастотного фильтров, причём wФНЧ > wФВЧ. Заграждающие фильтры формируют параллельным соединением низкочастотного и высокочастотного фильтров, причём wФВЧ > wФНЧ. Параметры элементов фильтров, составляющих ПФ или ЗФ, подбирают так, чтобы L1С1 = L2С2.
Тогда резонансная частота и волновое сопротивление у обоих фильтров будут:
w1∙w2 = w02 ; w0 =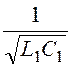 =
=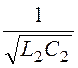 ;
ρ = ZС(w0) =
;
ρ = ZС(w0) =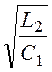 =
=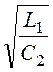 .
.
Относительная (или нормированная) частота здесь обозначается и определяется несколько иначе, чем у других фильтров:
Ω =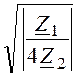 или Ω=
или Ω=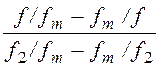 , fт =
, fт =![]() .
.
Граничные частоты полосы пропускания, характеристическое сопротивление и элементы полосового фильтра определяются выражениями:
f 1,2 =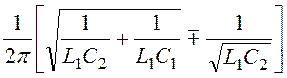 ; ZС(Ω)
= ±
; ZС(Ω)
= ±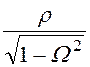 .
.
L1 =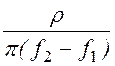 ;
L2 =
;
L2 =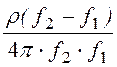 ;
;
С1 =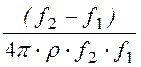 ; С2
=
; С2
=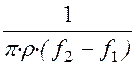 .
.
Граничные частоты полосы непропускания, характеристическое сопро-тивление и элементы заграждающего фильтра определяются выражениями:
f 1,2 = 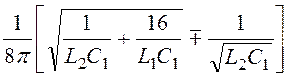 ; Zс(Ω) = ±
; Zс(Ω) = ±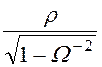 ;
;
L1 = 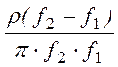 ;
L2 =
;
L2 =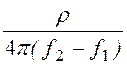 ;
;
С1 =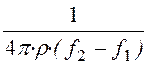 ;
С2 =
;
С2 =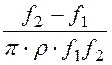 .
.
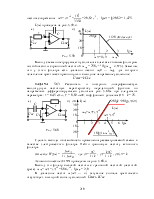
Задача 5.44. Фильтр низкой частоты собран из двух катушек с индуктивностью L1 = 0,5 Гн и одного конденсатора ёмкостью C2 = 10 мкФ. Фильтр подключен в сеть частоты f = 50 Гц, входное напряжение фильтра несинусоидальное u1(t) = 100·sinwt – 33,3·sin3wtB.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.