Частотные электрические фильтры. Основные теоретические положения, страница 5

Задача 5.54. Рассчитать конструктивные параметры высокочастот-ного последовательно преобразованного фильтра типа  m, имеющего гранич-ную частоту  f₀ = 100 Гц  и нагруженного сопротивлением  r_H = 200 Ом.  Па-раметр преобразования  m = 0,8.

Привести схему фильтра, рассчитать и построить его рабочие характеристики.

Решение

Так как фильтры типа  m  являются преобразованными из фильтров  k, то на первом этапе расчёта определим расчётные параметры симметричного фильтра типа  k.

Для высокочастотного фильтра типа  kρ == r_H ,    f₀ =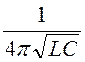, откуда расчётные параметры  L =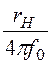==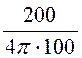 0,159 Гн,

C =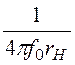==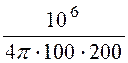 3,98 мкФ.

Улучшенными свойствами по согласованию при последовательном преобразовании обладает П-схема фильтра m, продольное сопротивление которого

Z_1m = mZ₁ = m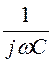==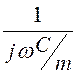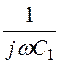, откуда для фильтра  m     C₁ === 4,98 мкФ.

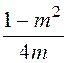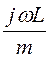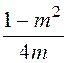
Поперечное сопротивление фильтра  m при последовательном преобразовании     Z_2m =+Z₁, откуда для высокочастотного фильтра  Z_2m =+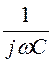=jωL₂ +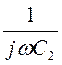, а числовые значения    L₂ = L/m= 0,159/0,8 = 0,199 Гн,

С₂ =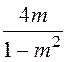С =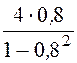·3,98 = 35,4 мкФ.

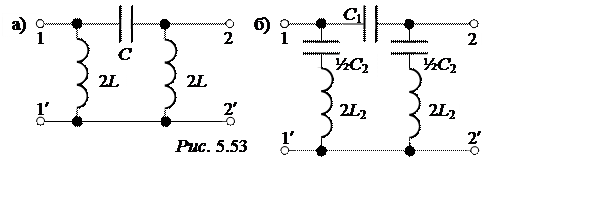
На рис. 5.53,а приведена П-схема фильтра  k, а на рис. 5.53,б – П-схема последовательно преобразованного фильтра типа  m. На этих схемах указаны конструктивные параметры: для фильтра  k –  С = 3,98 мкФ,  2L = 0,318 Гн;

для фильтра  m –  С₁ = 4,98 мкФ,  ½С₂ = 17,7 мкФ,  2L₂ = 0,398 Гн.

Дополнительная резонансная частота

ω₀¢ = ω₀==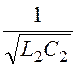= 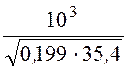376,8 c ^-1,

f₀¢ ===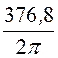 60 Гц.

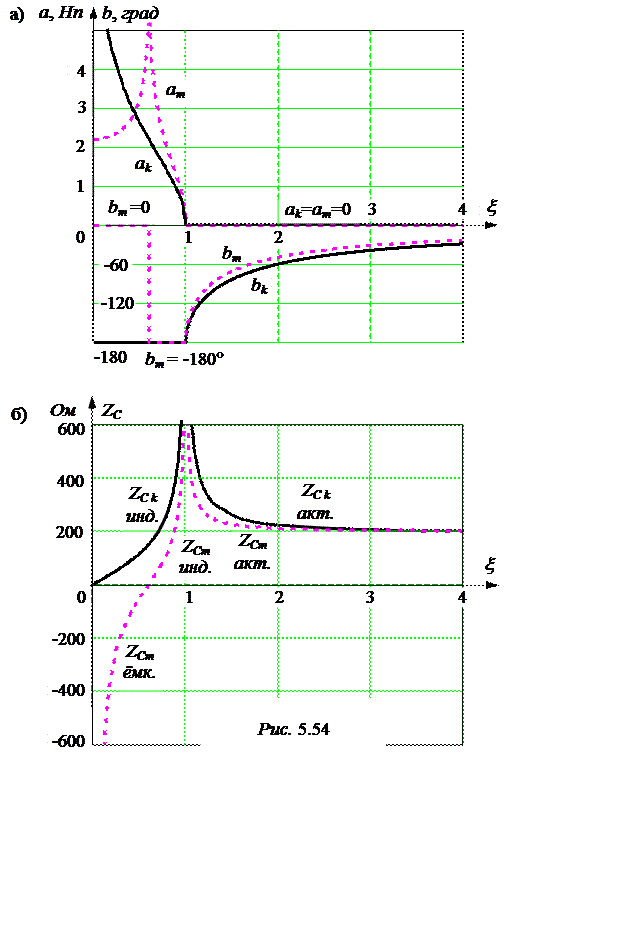
Результаты расчёта рабочих характеристик сведены в табл. 5.7, причём расчёты произведены на основании формул 

chГ = ch(a + jb) = 1 +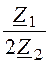,       Z_CП =.

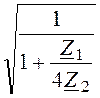Эти формулы справедливы как для фильтра  k, так и фильтра  m, если

Z₁ – продольное расчётное сопротивление, Z₂ – поперечное расчётное сопро-тивление.

Рабочие  характеристики  a(x), b(x) построены на рис. 5.54,а,  Z_C(x) - на рис. 5.54,б.

Обращаем внимание на то, что  Z_1m  и  Z_2m  в диапазоне частот от нуля до  f₀¢= 60 Гц  имеют одинаковый знак и  chГ = ch(a + jb) = 1 +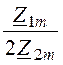> 0, что соот-ветствует  cos b= 0,  b= 0.

При f > f₀¢знак  Z_2m  меняется на обратный,   cos b= -1,   b= -p  – проис-ходит опрокидывание фазы (изменение её скачком на  p = 180°).

Задача 5.55. Для исходной Т-схемы высокочастотного фильтра, имеющего граничную частоту  f₀ = 100 Гц  и параметр нагрузки  k= 200 Ом определить расчётные параметры, привести схему фильтра.

Привести схему высокочастотного фильтра типа m с параллельной коррекцией, рассчитать параметры фильтра при  m= 0,8.

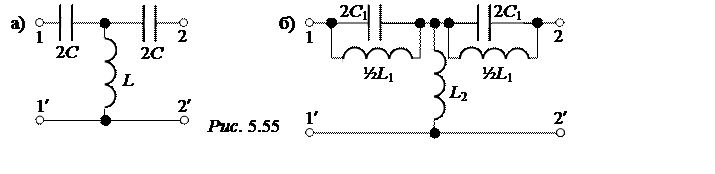Ответы: рис. 5.55,   L= 0,159 Гн,   С = 3,98 мкФ,

L₁ = 1,41 Гн,   С₁ = 4,975 мкФ,   L₂ = 0,199 Гн.

5.2.4. Пассивные  r-с фильтры

Принцип работы RС-фильтров базируется на изменении сопротивления ёмкости с частотой. В качестве частоты среза принимается частота, на которой равны сопротивления продольной и поперечной ветвей соответствующей Г-схемы фильтра:

ω_нчф =;                 ω_вчф =.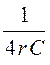

Выражения рабочих характеристик  а(ω), b(ω), Z_С(ω) получают анализом коэффициентов  А, В, С, D  соответствующей схемы фильтра-четырёхполюсника. Из формулы

chГ = ch(a + jb) = cha∙cosb + jsha∙sinb = М + jN, получают    cha =;

cosb =.

Характеристические сопротивления

Z_C1 =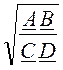=;                      Z_C2 ==.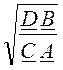

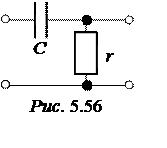Задача 5.56. Для Г-образного r-с фильтра высоких частот (рис. 5.56) с граничной частотой f₀ = 100 Гц выбран конденсатор ёмкостью 10 мкФ. Определить  rфильтра, а также рассчитать коэффициенты затухания и фазы и сопротивление   Z_2C  на частотах  50 Гц,  100 Гц,  150 Гц.

Решение

1. По определению, граничной частотой r-с фильтра считается частота, при которой равны продольное и поперечное сопротивления фильтра, то есть     r =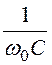==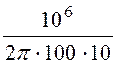 159,2 Ом.

2. Для получения характеристик затухания а(ω) и фазы b(ω),   необходимо исследовать величину   ch Г = ch(a + jb),   которая в случае несимметричного четырёхполюсника определяется по формуле   chГ =.

Коэффициенты А и D  Г-схемы определяем по формулам

А = 1 + Z₁/Z₂ = 1 +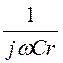,        D = 1.

Тогда       chГ ===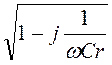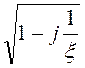,     где   ξ = ω/ω₀. 

Комплексную величину  chГ    представляем в алгебраической форме ch Г = М + jN,   после чего можно вычислить  cha   и   cosb   по следующим формулам:

ch a = ½  и