 Рассчитать мгновенное значение выходного напряжения,
исходя из условия, что на всех гармониках фильтр согласован с нагрузкой. Каким
при этом должно быть сопротивление нагрузки?
Рассчитать мгновенное значение выходного напряжения,
исходя из условия, что на всех гармониках фильтр согласован с нагрузкой. Каким
при этом должно быть сопротивление нагрузки?
Решение
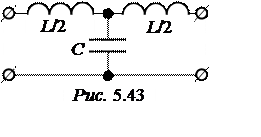
Из двух индуктивностей и одной ёмкости можно собрать только Т-схему низкочастотного фильтра (рис. 5.43). При этом расчётные параметры фильтра C =C2 = 10 мкФ,
L/2 =L1 = 0,5 Гн, L= 2L1 = 1 Гн.
Граничная частота фильтра w0 =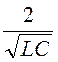 , f0 =
, f0 =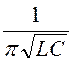 =
=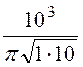 =
100,7 Гц.
=
100,7 Гц.
В режиме согласованной нагрузки
U1
= U2e Г = U2e а·e jb, ZH = ZCТ =![]()
![]() , где x =
, где x =![]() – относительная частота.
– относительная частота.
На частоте первой гармоники x =![]() =
=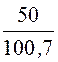 = 0,4965, характеристическое
сопротивление (оно же сопротивление нагрузки в согласованном режиме) ZH1 =
= 0,4965, характеристическое
сопротивление (оно же сопротивление нагрузки в согласованном режиме) ZH1 =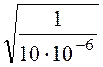
![]() = 274,5 Ом – активное
сопротивление. Заметим, что на этой частоте параметр нагрузки
= 274,5 Ом – активное
сопротивление. Заметим, что на этой частоте параметр нагрузки
k= ρ=![]() =
=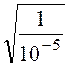 = 316 Ом > ZH1 = 274,5 Ом.
= 316 Ом > ZH1 = 274,5 Ом.
Частота первой гармоники f1 < f0 и эта гармоника принадлежит зоне прозрачности, на которой
a1 = 0, а b1 = arccos(1 - 2x 2) = arccos(1 – 2·0,4964 2) = 59,5°.
По условию U1m = U1m·e j·Yu1 = 100 B, тогда
U2m = U1m·e -Г = 100e –j59,5° B.
Мгновенное значение выходного напряжения первой гармоники
u2(1)(t) = Im(U2m·e jwt) = 100·sin(wt – 59,5°) B.
Для третьей гармоники x =![]() =
=![]() =
=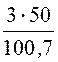 = 1,49.
= 1,49.
Сигнал этой частоты находится в полосе затухания ФНЧ, коэффициент фазы при этом b3 = p = 180°, коэффициент затухания
a3 = Arch(2x 2 – 1) = Arch(2·1,49 2 – 1) = 1,906 Нп.
Комплексная амплитуда выходного напряжения
U2m = U1m·e -Г = -33,3e –1,906·e j180° = 4,95 B, мгновенное значение выходного напряжения
u2(3)(t) = Im(U2m·e j3wt) = 4,95·sin(3wt) B.
Характеристическое сопротивление фильтра на третьей гармонике
ZH3 =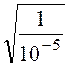
![]() = j349 Ом - индуктивное.
= j349 Ом - индуктивное.
Выходное напряжение фильтра при согласованных сопротивлениях нагрузки как на частоте w, так и частоте 3w
u2(t) = u2(1) + u2(3) = 100·sin(wt – 59,5°) + 4,95·sin(3wt) B.
Это напряжение практически синусоидально, так как третья гармоника подавлена:
U2m(3) = 4,95%U2m(1).
ЗАДАЧА 5.45. Рассчитать расчётные и конструктивные параметры П-схемы низкочастотного фильтра типа k, работающего на активную нагрузку rH= 200 Ом и имеющего граничную частоту f0 = 150 Гц.
Решение
Принимаем k =![]() = rH, w0 = 2pf0 = 6,28·150 = 942 c -1=
= rH, w0 = 2pf0 = 6,28·150 = 942 c -1=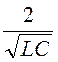 , получаем
расчётные параметры фильтра L =
, получаем
расчётные параметры фильтра L =![]() =
=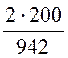 =
0,425 Гн,
=
0,425 Гн,
 С =
С =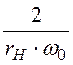 =
=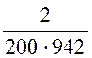 = 1,06·10 -5 Ф = 10,6 мкФ.
= 1,06·10 -5 Ф = 10,6 мкФ.
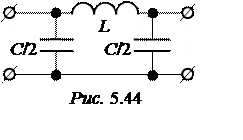
П-схема фильтра низкой частоты приведена на рис. 5.44. Конструктивные параметры фильтра
L = 0,425 Гн, ½С = 10,6/2 = 5,3 мкФ.
 ЗАДАЧА 5.46. Фильтр высоких частот собран из двух катушек с
индуктивностью L2 = 0,13 Гн и одного конденсатора ёмкостью С1= 10 мкФ. Фильтр подключен в
сеть частоты f = 50 Гц с несинусоидальным напряже-нием u1(t) =
100·sinwt
– 33,3·sin3wtB.
ЗАДАЧА 5.46. Фильтр высоких частот собран из двух катушек с
индуктивностью L2 = 0,13 Гн и одного конденсатора ёмкостью С1= 10 мкФ. Фильтр подключен в
сеть частоты f = 50 Гц с несинусоидальным напряже-нием u1(t) =
100·sinwt
– 33,3·sin3wtB.
Привести схему ФВЧ, рассчитать выходное напряжение, исходя из условия, что на всех гармониках фильтр согласован с нагрузкой.
Ответ: рис. 5.45,
u2(t) = -7,35·sinwt – 33,3·sin(3wt + 90°) B.
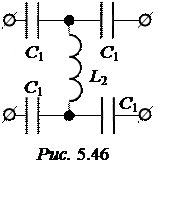 ЗАДАЧА 5.47. В системе связи по распредели-тельным сетям (до 1000
В при частоте 50 Гц) передаю-щую и приёмную аппаратуру защищают
от напряжения сети уравновешенным Т-образным высокочастотным фильтром
типа k (рис. 5.46) (передача сигналов
связи осуществляется модулированными колебаниями на не-сущей частоте, большей,
чем частота напряжения сети).
ЗАДАЧА 5.47. В системе связи по распредели-тельным сетям (до 1000
В при частоте 50 Гц) передаю-щую и приёмную аппаратуру защищают
от напряжения сети уравновешенным Т-образным высокочастотным фильтром
типа k (рис. 5.46) (передача сигналов
связи осуществляется модулированными колебаниями на не-сущей частоте, большей,
чем частота напряжения сети).
Ёмкость каждого конденсатора С1= 0,15 мкФ, характеристическое сопротивление фильтра с увеличением частоты приближается к r = 600 Ом. Найти граничную частоту фильтра и коэффи-циент затухания на частоте сети.
Решение
Определим расчётный параметр фильтра С: при последовательном соединении двух ёмкостей одного плеча Т-схемы четырёхполюсника
СЭ = ½С1, что соответствует 2С типовой схемы высокочастотного фильтра, откуда расчётная величина С = ½СЭ = ¼С1= 0,15/4 = 0,0375 мкФ.
Параметр нагрузки k =![]() = r,
откуда расчётная индуктивность фильтра L= r 2·С
= 600 2·0,0375·10
-6 = 13,5·10 -3 Гн.
= r,
откуда расчётная индуктивность фильтра L= r 2·С
= 600 2·0,0375·10
-6 = 13,5·10 -3 Гн.
Граничная частота фильтра (частота среза)
w0 =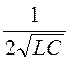 , f0 =
, f0 =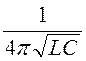 =
=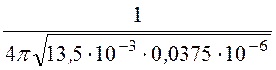 =
3,54·10 3 Гц.
=
3,54·10 3 Гц.
Коэффициент затухания на частоте сети
a
= Arch(![]() – 1)
= Arch(2
– 1)
= Arch(2![]() – 1) = Arch
– 1) = Arch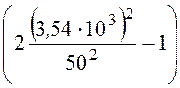 = 9,906 Нп.
= 9,906 Нп.
При напряжении сети U1= 1000 B частоты f=
50 Гц и
согласованной с фильтром нагрузке U2 =![]() =
= = 0,05 B.
= 0,05 B.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.