Частотные электрические фильтры. Основные теоретические положения, страница 6

cosb = ½.  

Характеристическое сопротивление  Z_2C  находим следующим образом:

Z_2Х = r,      Z_2К = r/(1 + jωСr) ;   

Z_2C ===.  

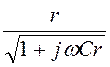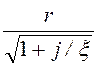Результаты расчётов характеристик Г-фильтра сводим в табл. 5.8.

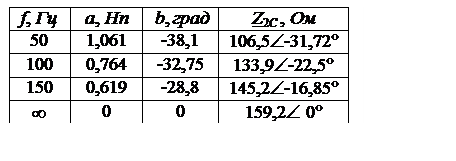
Таблица 5.8

ЗАДАЧА 5.57. Составить низкочастотный  фильтра по симметричной Т-схеме с граничной частотой  f₀ = 20 Гц  для работы на активную нагрузку  r_H  = 630 Ом.

На частотах  f₁ = 0,5f₀,  f₂ = f₀,  f₃ = 2f₀  определить коэффициенты затухания и фазы фильтра, а также его характеристическое сопротивление.

Решение

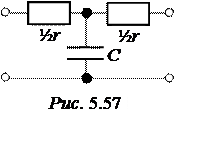
На рис. 5.57 представлена схема симметричного Т-образного низко-частотного  фильтра. Расчётное сопротивление фильтра r определяется из условия передачи максимума мощности со входа на выход при частоте  f = 0, что соответствует равенству  r  = r_H  = 630 Ом.

Конструктивный параметр ½r фильтра рис. 5.57     ½r= 630/2 = 315 Ом.

Граничная частота  r-с  фильтра определяется равенством продольного и поперечного сопротивлений Г-образного полузвена:  ½r=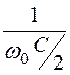,  откуда  w₀ =  и расчётная ёмкость фильтра  С ===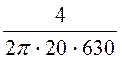 50,53 мкФ.

Коэффициенты затухания  а  и фазы  bдля  r-с фильтра рассчитываются на основании общего выражения коэффициента  А симметричных Т- или П-схем четырёхполюсников с половинными параметрами Г-образного полузвена:

chГ = А 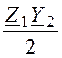= 1 += 1 +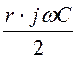= 1 + j2x, где x  = - относительная частота.

С другой стороны,  chГ = ch(а + jb) = chа×cosb + jshа×sinb = M + jN,   где  M= Re(chГ),  N= Im(chГ).

Получаем систему уравнений     chа×cosb = M,

shа×sinb = N, откуда    cha = ½,

cosb = ½.

Характеристическое сопротивление симметричной Т-схемы

Z_CT ====.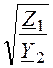

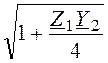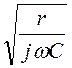
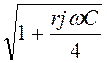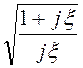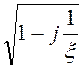Результаты расчёта характеристик представлены в табл. 5.9.

Таблица 5.9

w	x	M	N	cha	a, Нп	cosb	b, град	ZC , Ом
w= 0,5w0	0,5	1	1	1,62	1,063	0,618	51,83	704Ð-31,72°
w= w0	1	1	2	2,41	1,527	0,414	65,54	445Ð-26,56°
w= 2w0	2	1	4	4,24	2,123	0,236	76,35	352Ð-13,28°

Задача 5.58. Из двух резисторов по   200 Ом   и одного конденсатора 4 мкФ собрали высокочастотный симметричный фильтр. Рассчитать его граничную частоту.

Ответ:   f₀ = 24,87 Гц.

Задача 5.58. Для Г-схемы низкочастотного фильтра рис. 5.28,а задачи 5.37 на основании логарифмической амплитудной частотной характеристики рис. 5.30,а определить граничную частоту фильтра.

Ответ:   w₀==== 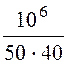500 c ^-1.

Задача 5.58. Г-схема низкочастотного фильтра предыдущей задачи нагружена постоянным сопротивлением r_H как показано на рис 5.33 задачи 5.39. Рассчитать граничную частоту фильтра на основании передаточной функции. Сравнить с режимом холостого хода предыдущей задачи.

Ответ:  у фильтра,   нагруженного неизменным сопротивлением  r_H = = 150 Ом, граничная частота  w₁===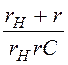= 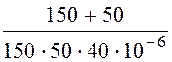667 c ^–1> w₀.

Задача 5.61. Симметричный Т-фильтр рис. 5.57 задачи 5.57 нагружен неизменным сопротивлением  r = ρ = 630 Ом. Составить передаточную функ-цию фильтра по напряжению, определить с её помощью граничную частоту фильтра, сравнить её с расчётной.

Ответ:

H(jw) =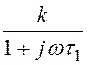,   где k =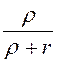= 0,5,  t₁=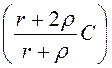= 11,94×10 ^–3 c, граничная частота фильтра  w₁===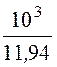 83,77 c ^–1,

f₁===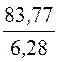 13,33 Гц.

5.2.5. Активные фильтры r-с

Активные фильтры построены на основе операционного усилителя (ОУ) напряжения, работающего с отрицательной обратной связью (ООС). Принципиальная схема такого четырёхполюсника приведена на рис. 5.58,а, соответствующая расчётная схема – на рис. 5.58,б.

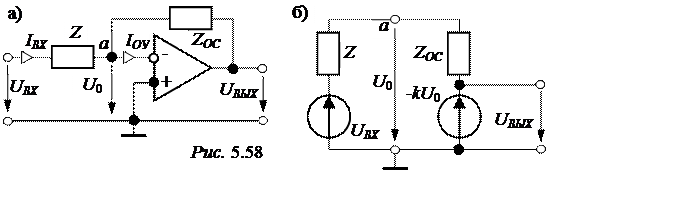Дифференциальный вход (-) …(+) усилителя имеет очень большое входное сопротивление, для идеального ОУ это сопротивление  R_BX = ¥, а поэтому входной ток   I_ОУ = 0.

Выходное сопротивление ОУ мало и для идеального ОУ  R_BЫX = 0, поэтому выходное напряжение U_BЫX не зависит от тока нагрузки и  U_BЫX = -kU₀, где  k– коэффициент усиления ОУ.