Частотные электрические фильтры. Основные теоретические положения, страница 4

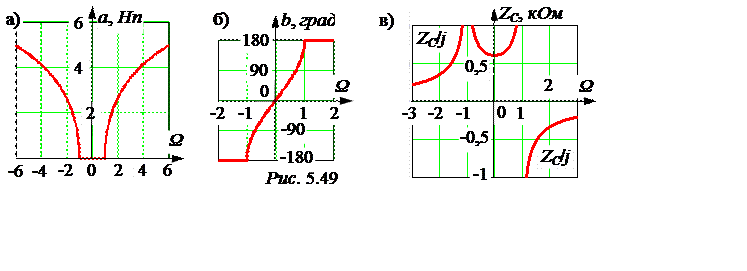
Графики характеристик  а(Ω),  b(Ω),  Z_С(Ω) представлены на рис. 5.49. В характеристиках а(Ω),  b(Ω),  Z_С(Ω) отсчёт  ±Ω  идёт в обе стороны от линии  ω₀.  В графиках зависимостей  а(f),  b(f),  Z_С(f) частота  f  отсчитывается от нуля и только в положительную сторону. Эти графики можно построить самостоятельно. Но они имеют привычный, типовой вид и практически не отличаются от приведенных, если мысленно перенести ось отсчёта в начало координат.

5.2.3. Фильтры типа m

Фильтры типа т имеют улучшенную характеристику сопротивления Z_C(ω) в зоне пропускания фильтра и повышенную крутизну характеристики а(ω) вблизи частоты среза фильтра. Фильтры типа т  получают из фильтров типа k введением последовательного или параллельного корректирующего звена  L_К  или  С_К. Чтобы при этом сохранялась частота среза исходного k-фильтра, одновременно изменяют остальные элементы фильтра.

При последовательной коррекции в т-раз изменяется продольное сопротивление фильтра:                      Z_1т = т∙Z_1k.

Поперечная ветвь фильтра будет иметь два последовательно соединённых элемента, которые рассчитываются по выражению 

Z_2т =+ Z_1k∙.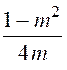

Последовательная коррекция влияет на частотную зависимость характеристического сопротивления П-схемы,делая его почти неизменным в зоне пропускания фильтра:   Z_СП(ω) » ρ.

При параллельной коррекции в т раз изменяется проводимость поперечной ветви фильтра:                Y_2т = т∙Y_2k.

Продольная ветвь фильтра будет иметь два параллельно соединённых элемента, проводимости которых рассчитываются по выражению 

Y_1т = + Y_2k∙.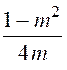

Параллельная коррекция влияет на характеристическое сопротивление Т-схемы,делая его почти неизменным в зоне пропускания фильтра: Z_СТ(ω)»ρ.

ЗАДАЧА 5.52.   Задана   Т-схема   низкочастотного   фильтра   типа   k (рис. 5.50,а) с расчётными параметрами   L = 9,63 Гн,  С = 26,74 мкФ.   Рас-считать и построить его частотные характеристики   a_k(x),  b_k(x),  Z_CTk(x),  где x = –  относительная частота.

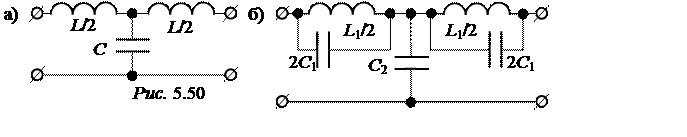Рассчитать параметры Т-схемы фильтра типа m с улучшенными свойствами по согласованию фильтра с нагрузкой в зоне прозрачности и построить для него частотные характеристики  a_m(x),  b_m(x),  Z_CTm(x). Пара-метр преобразования принять равным  m = 0,8.

Решение

Для исходного фильтра типа k (рис. 5.50,а)

граничная частота      ω₀ =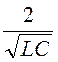==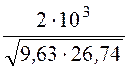 124,6 c ^-1, параметр нагрузки     k ===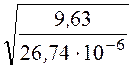 600 Ом.

Характеристическое сопротивление  Z_CTk = –  для всех частот;

коэффициент затухания  a_k= 0  при  x £ 1,           a_k= Arch(2x ² – 1)  при  x > 1, коэффициент фазы  b_k= arccos(1 – 2x ²) при  x £ 1,  b_k= +p = +180°  при  x > 1.

Поперечная проводимость преобразованного фильтра

Y_2m = m·Y_2k = m·jωC = jωC₂, расчётная ёмкость фильтра типа m (рис. 5.50,б)

C₂ = m·C = 0,8·26,74 = 21,39 мкФ.

Расчётная проводимость параллельного контура фильтра  типа   m  (рис. 5.50,б)    Y_1m =+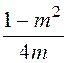Y_2k =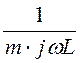+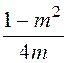·jωC =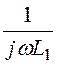+ jωC₁, откуда новое значение индуктивности    L₁ = mL = 0,8·9,63 = 7,704 Гн, ёмкости              С₁ =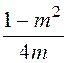С =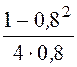·26,74 = 3 мкФ, резонансная частота параллельного контура без потерь (рис. 5.44,б)

ω₀¢ =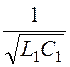==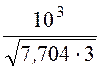 208 c ^-1,    x ===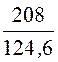 1,67

безусловно принадлежит зоне затухания.

Так как на этой частоте сопротивление параллельного контура без потерь бесконечно большое, коэффициент затухания на этой частоте также бесконечно большой.

Расчёт частотных характеристик фильтра типа m произведём на основании общих соотношений для Т-схемы фильтра:

chГ_m = ch(a_m + jb_m) = 1 +,    Z_CTm =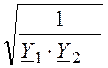 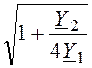, где          Y₁ =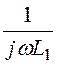+ jωC₁,       Y₂ =  jωC₂.

Результаты расчётов характеристик фильтров  k и  m  сведены в общую табл. 5.6.

На рис. 5.51,а приведены характеристики  a(x),  b(x);

на рис. 5.51,б – характеристики   Z_C(x).

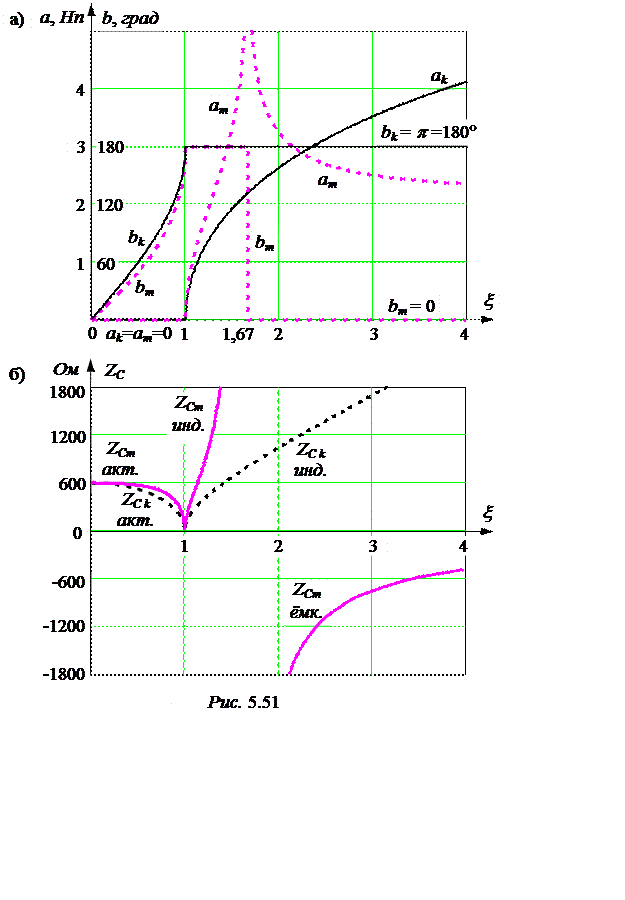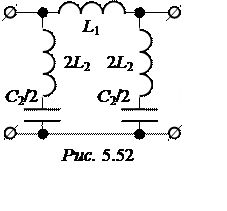ЗАДАЧА 5.53. Рассчитать параметры П-схемы низкочастотного фильтра типа  m с улучшенными свойствами, взяв за основу схему рис. 5.44 фильтра типа  k и его расчётные параметры

L = 0,425 Гн,  С = 10,6 мкФ.

Принять коэффициент преобразования m= 0,6.

Привести схему фильтра типа  m. Определить постоянную передачи фильтра  на частоте  w = 1,1w₀.

Ответы:  рис. 5.52 (L₁ = 0,255 Гн,  С₂ = 6,36 мкФ,  L₂ = 0,113 Гн),

a= 1,563 Нп,   b= p = 180°.