Частотные электрические фильтры. Основные теоретические положения, страница 7

Знак (-) учитывает то обстоятельство, что из-за подачи сигнала на инвертирующий вход полярность выходного напряжения противоположна полярности напряжения U₀ на дифференциальном входе ОУ.

Рассчитаем передаточную функцию активного четырёхполюсника по схеме рис. 5.58,б.  По методу узлового напряжения    U₀ =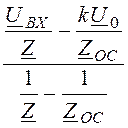, откуда  U₀·(Z+ Z_oC) = U_BXZ_oC– kU₀Z     и    U₀ =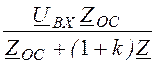, а  U_BЫX = -kU₀ = -U_BX.

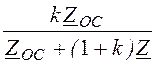Передаточная функция по напряжению

H(jw) =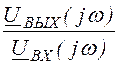=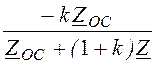, на основе которой изучаются свойства активных электрических фильтров.

ЗАДАЧА 5.62. Рассчитать и построить асимптотическую логарифмическую амплитудную частотную характеристику передаточной функции по напряжению интегрирующего усилителя рис. 5.59,а при следующих параметрах:  r = 4,3 кОм,  С = 0,3 мкФ,  k= 25.Сделать выводы о возможности применения рассмотренной схемы в качестве электрического фильтра. Найти граничную частоту активного фильтра.

Решение

Передаточная функция по напряжению четырёхполюсника рис. 5.59,а

H(jw) =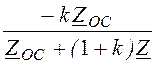==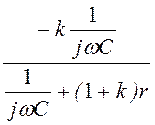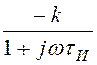, где постоянная времени реального интегрирующего звена

t_И = (1 + k)rС = (1 + 25)×4,3×10³×0,3×10 ^-6 = 33,54×10 ^–3 с.

Амплитудная частотная характеристика передаточной функции

H(w) =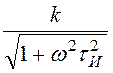,   её ЛАЧХ    L(w) = 20lgH(w) = 20lgk – 10lg(1 + w²t_И²)

причём   20lgk = 20lg25 = 28 дБ, частота сопряжения   w_И = t_И ^–1 =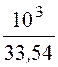= 29,82 с ^-1,    lgw_И = lg29,82 = 1,475.

L(w) приведена на рис. 5.59,б.

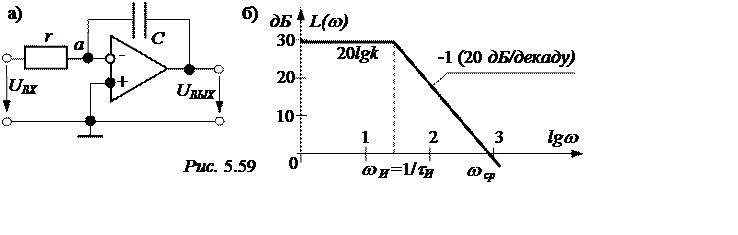Вывод: схема интегрирующего усилителя является активным фильтром низкой частоты с граничной частотой  w _cp = 750 с ^–1   (lgw _cp = 2,875). Заметим, что у этого фильтра есть диапазон частот w(0 … w_И), для которого ослабление практически равно нулю и выходное напряжение усиленное:

U_BЫX = kU_BX.

ЗАДАЧА 5.63. Рассчитать и построить логарифмическую амплитудную частотную характеристику передаточной функции по напряжению дифференцирующего усилителя рис. 5.60,а при следующих параметрах:  r = 64,5 кОм,  С = 0,02 мкФ, коэффициент усиления ОУ   k = 25.

Сделать выводы о возможности применения рассматриваемой схемы в качестве электрического фильтра. Найти граничную частоту активного фильтра.

Ответы: H(jw) = -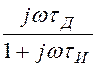,  где  t_И =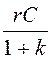,   t_Д =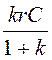,  t_Д /t_И = k.

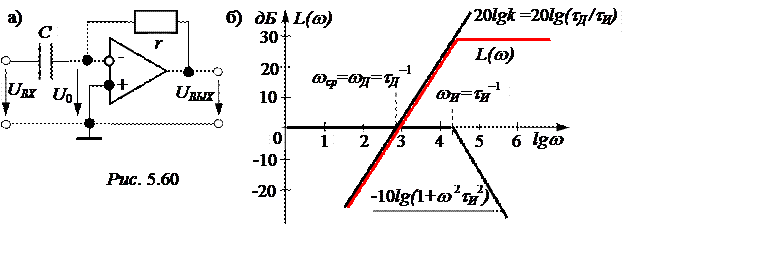
Асимптотические ЛАЧХ приведены на рис. 5.60,б.

Вывод: это фильтр высокой частоты с граничной частотой (частотой среза)  w _cp = w_Д  = t_Д ^–1 = 806 с ^–1,  lgw_ср = 2,9.

В диапазоне частот w(w_И… ¥) затухание сигнала практически отсутствует, выходной сигнал усиленный  U_BЫX » kU_BX.

ЗАДАЧА 5.64. Рассчитать и построить логарифмическую амплитудную частотную характеристику передаточной функции по напряжению высокочастотного активного фильтра рис. 5.61,а при следующих параметрах:  r = 4,3 кОм,  С = 0,02 мкФ,   k = 25,  n = 15.

Найти граничную частоту фильтра w _сp. Определить ослабление сигнала на двух частотах:  w ₁ = 30 с ^–1,  w ₂ = 300 с ^–1.

Решение

Расчётная схема устройства рис. 5.61,а приведена на рис. 5.61,б, откуда

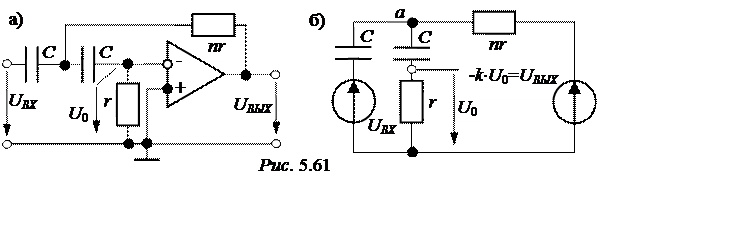j _а ==,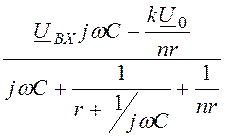

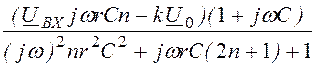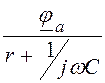U₀ =×r =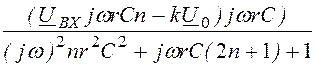,  U_BЫX = -k×U₀,

H(jw) =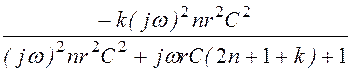   или

H(jw) =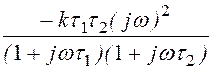,   где

t₁t₂ = nr²C² = 15×4,3²×10⁶×0,02²×10 ^-12 = 1109,4×10 ^–10,

t₁ + t₂ = (2n + 1 + k)rC = (30+1+25)×4,3×10³×0,02×10 ^-6 = 481,6×10 ^–5, откуда    t₁ = 479,3×10 ^–5 c,        t₂ = 2,3×10 ^–5 c,

w_t1 = t₁^-1 = 208,6 c ^-1,   w_t2 = t₂^-1 = 43200 c ^-1,

lgw₁ = 2,32,                 lgw₂ = 4,64.    

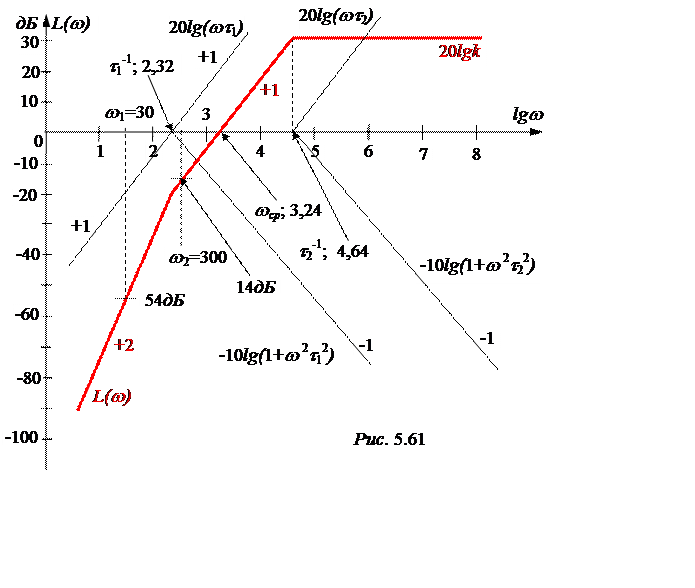
Логарифмическая амплитудная частотная характеристика  функции  приведена на рис. 5.61, причём

L(w) = 20lgk + 20lg(wt₁) + 20lg(wt₂) – 10lg[1 + w²t₁²] – 10lg[1 + w²t₂²].

Граничная частота фильтра в соответствии с рис. 5.56

w_cp = 10^3,24 = 1738 c ^-1,    f_cp = 276,6 Гц.

При частоте  w₁ = 30 c ^–1

ослабление сигнала по амплитуде  а₁ = 54 дБ = 6,21 Нп, при частоте  w₂ = 300 c ^–1    –   а₂ = 14 дБ = 1,61 Нп.

ЗАДАЧА 5.65. Рассчитать и построить логарифмическую амплитуд-ную частотную характеристику передаточной функции активного фильтра низкой частоты рис. 5.63 при следующих параметрах:

r = 4,3 кОм,  С = 0,02 мкФ,   k = 25,  n = 15.

Определить граничную частоту фильтра  w_cp. Определить граничную частоту  w₁, до которой у сигналов частот  w(0 … w₁) сохраняется пропор-циональность между реакцией и воздействием –   U_BЫX » kU_BX.

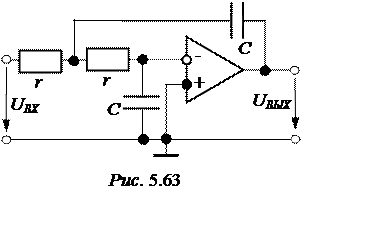Ответы:   w_cp = 741 c ^-1;   w ₁ = 29,5 с ^-1.