Частотные электрические фильтры. Основные теоретические положения, страница 3

Задача 5.48. Для фильтра низких частот типа k известно, что его номинальное характеристическое сопротивление   k = 600 Ом,  а затухание на частоте   f  = 5,6 кГц  должно быть не ниже 20 дБ.

Определить частоту среза и конструктивные параметры Т- и П-схем ФНЧ.

Ответы:  f₀ = 3,22  кГц;   расчётные параметры L= 59,3 мГн;

С = 0,165 мкФ.

Задача 5.49. Для подавления помехи на частоте 64 кГц и пропускания сигналов более высоких частот применён П-образный фильтр типа k с граничной частотой 96 кГц. Для фильтра выбран конденсатор ёмкостью 4·10 ³  пФ. Какой индуктивности должны быть катушки?

Достаточно ли одного фильтра для ослабления мешающего сигнала на 40 дБ? Сколько звеньев для этого должен содержать фильтр?

Ответы:  Две катушки по 0,344 мГн. Недостаточно. Три звена.

ЗАДАЧА 5.50. Задан полосовой фильтр присоединения (рис. 5.47,а), с помощью которого к линии высокого напряжения (свыше 1000 В) при час-тоте сети 50 Гц подключают аппаратуру диспетчерской связи для передачи сигналов. Параметры фильтра С₁ = С₂ = 1100 пФ,  L₁ = L₂ = 4,84 мГн. Опреде-лить коэффициент связи катушек, при котором полоса пропускания сигнала фильтром составит  55 ÷ 110 кГц.

Решение

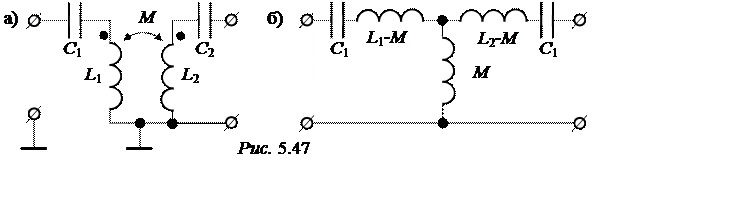
Устранив индуктивную связь катушек, получим Т-образную схему замещения (рис. 5.47,б). Это – симметричная схема  Т-фильтра рис. 5.2,а, для которой

сhГ = А = 1 += 1 +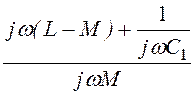, где    С₁ = С₂ = С = 1,1·10 ^-3 пФ,  L₁ = L₂ = L = 4,84 мГн,   М = k_СВ= k_СВL,

k_СВ  – искомый коэффициент связи.

В полосе пропускания затухание  а = 0,

сhГ = сh(jb) = cos b = 1 – .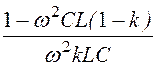

Границы зоны прозрачности полосового фильтра определяются значе-ниями

сosb = ±1.

Положив  сosb = +1, получим правую границу зоны прозрачности

ω₂ =;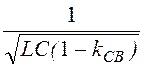

при сos b = -1, получим левую границу зоны прозрачности ω₁ =.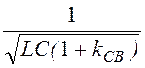

Тогда   1 – k_СВ=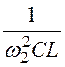==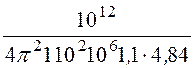 0,394,

1 + k_СВ =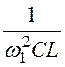==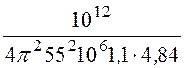 1,574,

k_СВ = (1,574 – 0,394)/2 = 0,59.

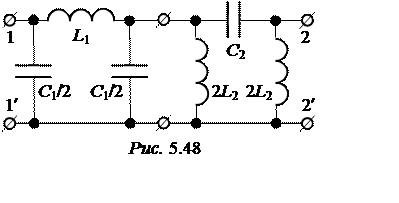
ЗАДАЧА 5.51. Частоты среза П-образного полосового фильтра типа k (рис. 5.48)

f₁ = 12 кГц,    f₂ = 15,2 кГц, номинальное характеристическое сопротивление 600 Ом.

Найти параметры элементов фильтра и построить его частотные характеристики в функции нормированной (относительной) частоты Ω, т.е. кривые  а(Ω),  b(Ω),  Zс(Ω), сравнив их с характеристиками в функции  f-частоты: а(f), b(f), Zс(f).

Решение

Рассчитываем параметры элементов фильтра:

L₁ =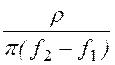==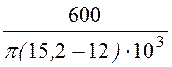 0,06 Гн;

L₂ =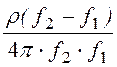==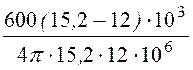 0,84×10 ^-3 Гн = 0,84 мГн; 

С₁ = 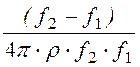==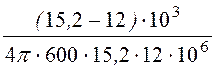 2,33×10 ^-9 Ф = 2,33 нФ;

С₂ =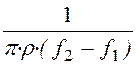==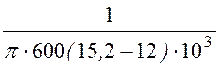 0,167×10 ^-6 Ф = 0,167 мкФ.

В диапазоне частот от 0 до ∞ полосовые фильтры имеют сначала зону затухания, затем зону пропускания и вновь зону затухания сигнала. Поэтому рабочие характеристики здесь строят влево и вправо от резонансной частоты ω₀, а не от нуля, как принято при построении характеристик в функции частоты f. Относительная (или нормированная) частота Ω здесь определяется выражением  

Ω=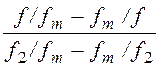,   где   f_т === 13,5 кГц.

Формулы для построения рабочих характеристик полосового фильтра:

- в зоне прозрачности      а = 0;                          b = 2arcsin Ω; 

- в зоне задерживания      а = 2Arch |Ω|;            b  =π; 

- выражение  Z_С(Ω) = ±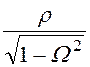 справедливо во всём диапазоне частот.

Расчёты, связанные с построением частотных характеристик, сводим в табл. 5.5.

Таблица 5.5  

Полоса	f, кГц	Ω	а, Нп	b, град	ZС, Ом
Задерживания	0	-∞	∞	-180°	0
	4	-13	6,52	-180°	j46,1
	8	-4,65	4,44	-180°	j132
	12	-1,0	0	-180°	∞
Пропускания	13	-0,316	--	-37°	632
	13,5	0	--	0°	600
	14	+0,316	--	+37°	632
	15,2	1,0	0	+180°	∞
Задерживания	18	2,46	3,1	+180°	-j268
	20	3,4	3,8	+180°	-j185