Методические указания к лабораторным работам по курсу “Компьютерная графика”

Министерство образования и неуки  Российской Федерации

Государственное образовательное учреждение

высшего профессионального образования

Комсомольский – на – Амуре Государственный Технический Университет

Кафедра vматематического обеспечения и применения ЭВМ

ФРАКТАЛЬНАЯ ГРАФИКА

Методические указания к лабораторным работам по курсу

“Компьютерная графика”

для студентов специальности 010503

Комсомольск – на – Амуре 2005

ВВЕДЕНИЕ

В данном методическом пособии будут рассмотрены фрактальные множества и методы отображения этих множеств на экране компьютера.

Если топология изучает свойства геометрических фигур, инвариантные при гомеоморфизмах, то фрактальная геометрия изучает свойства, инвариантные относительно подобий. Одним из самых важных инвариантов является размерность Хаусдорфа-Безиковича. Этой теме посвящены начальные параграфы. Затем вводится определение фрактала, дается классификация фракталов и приводятся примеры. Изучается метод построения фракталов с помощью итерируемых систем функций: ковер Серпинского, кривая Серпинского, кривая Коха. Рассматривается ящичная (box-counting) размерность, на основе которой вычисляется размерность Хаусфорда-Безиковича некоторых фрактальных множеств. Последний параграф посвящен алгебраическим фракталам: областям Жюлиа и областям притягивания корней уравнения относительно преобразования Ньютона.

Рекомендуемая литература: /9,11-12,24-26/.

1. Метрические пространства

Данный параграф посвящен полным метрическим пространствам и их примерам, имеющим важное значение во фрактальной геометрии.

Ниже повсюду  обозначает множество всех вещественных функций,  – -мерное евклидово пространство, при натуральных .

Метрическим пространством называется пара (), состоящая из произвольного множества  и функции , принимающей для всех неотрицательные значения  и удовлетворяющей условиям:

(М1)       тогда и только тогда, когда ;

(М2)       при любых ;

(М3)       при любых .

Фунция  называется метрикой, а ее значение  - расстоянием между .

Пример 1.  с метрикой

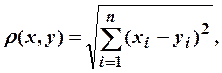
при  и , будет метрическим пространством, условие (М3) доказывается с помощью неравенства Коши-Буняковского. Каждое подмножество  с этой метрикой будет метрическим пространством.

Пусть  - метрическое пространство. Подмножество  называется ограниченным, если существует число  такое, что для всех элементов  имеет место неравенство . Верхняя грань чисел , где  и  пробегают множество , называется диаметром множества  и обозначается . Ясно, что если  , то  ограничено. Поскольку верхнюю грань имеет произвольное ограниченное подмножество из , то верно и обратное – ограниченное подмножество имеет конечный диаметр. Шаром радиуса  с центром в  называется подмножество

.

Точка  называется предельной точкой множества , если для каждого  шар  содержит бесконечное число точек множества .

Подмножество  называется замкнутым, если оно содержит все свои предельные точки.

Для любого подмножества  и произвольного элемента  положим .

Метрика Хаусдорфа на множестве всех ограниченных замкнутых подмножеств  метрического пространства  определяется формулой

.

Пара  будет метрическим пространством.

Пример 2. Пусть  - евклидово пространство с обычной метрикой. Для производльного  подмножества  дилитацией множества  называется множество

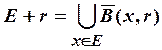, где  - замкнутый шар радиуса  с центром в точке . Тогда расстояние Хаусдорфа между любыми замкнутыми ограниченными подмножествами  будет равно

.

Пусть  - метрическое пространство. Последовательность  называется сходящейся в себе или фундаментальной последовательностью, если .

Элемент называется пределом последовательности  и обозначается , если

Легко видеть, что каждая последовательность, имеющая предел, сходится в себе. Метрическое пространство  называется полным, если каждая сходящаяся в себе последовательность элементов  имеет предел в .

Пример 3. Пусть  - замкнутое ограниченное подмножество. Тогда , расстояния между точками которого определяются с помощью метрики пространства , является полным метрическим пространством.

Отображение метрического пространства  в себя называется сжатием, если существует неотрицательное число  такое, что для всех  имеет место неравенство .

Принцип сжатых отображений. Пусть  - полное метрическое пространство,  - сжатие. Тогда существует единственный элемент  такой, что .

Пусть  - полное ограниченное метрическое пространство,  - множество его замкнутых подмножеств с метрикой Хаусдорфа

.

Тогда для любой фундаментальной последовательности  в метрическом пространстве  ее предел можно вычислить как 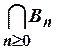, где  Здесь  обозначает наименьшее замкнутое множество, содержащее множество . Отсюда вытекает, что  в этом случае будет полным метрическим пространством. Заметим, что для последовательности замкнутых ограниченных подмножеств произвольного полного метрического пространства  ее предел относительно метрики Хаусдорфа будет равен .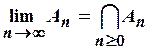

Подмножество  метрического пространства  называется открытым, если для каждой точки  существует такое число , что шар  целиком содержится в . Хорошо известно, что множество  является открытым тогда и только тогда, когда его дополнение  замкнуто.