· Разделим
![]() -мерное евклидово пространство сетью
клеток, состоящей из
-мерное евклидово пространство сетью
клеток, состоящей из ![]() -мерных кубов со стороной
-мерных кубов со стороной ![]() Пусть
Пусть ![]() обозначает
число клеток, имеющих непустое пересечение с
обозначает
число клеток, имеющих непустое пересечение с ![]() . Тогда
. Тогда
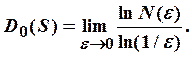
Например, для ковра Серпинского, при 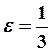 имеем
имеем 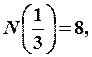 при
при 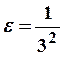 в каждом из восьми квадратов будет
содержаться восемь квадратов, пересекающихся с ковром, значит,
в каждом из восьми квадратов будет
содержаться восемь квадратов, пересекающихся с ковром, значит, 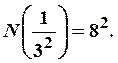 При любом натуральном
При любом натуральном ![]() и
и 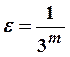 получаем
получаем
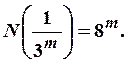 Следовательно,
Следовательно, 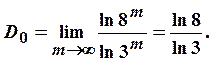
 Пример 8. Кривая
Серпинского. Рассмотрим прямоугольный треугольник, длина катетов которого
равна 1. Разобъем его на 4 равных треугольника, как это показано на рис. 6 и
удалим средний треугольник.
Пример 8. Кривая
Серпинского. Рассмотрим прямоугольный треугольник, длина катетов которого
равна 1. Разобъем его на 4 равных треугольника, как это показано на рис. 6 и
удалим средний треугольник.
Затем эту процедуру применим к каждому из оставшихся треугольников и т.д. В пределе получим множество, которое называется кривой Серпинского и обладает рядом замечательных свойств: его площадь равна нулю, длина периметра этого множества равна бесконечности и т.д.
Приведем текст программы, выводящий фигуру, полученную после нескольких шагов.
//Кривая Серпинского serp5k.cpp
#include <graphics.h>
#include <conio.h>
float xmin = -0.5, xmax = 1.5, ymin = -0.5, ymax = 1.5;
int ex(float x)
{ return (int)((x-xmin)/(xmax-xmin)*(getmaxx()+1));}
int ey(float y)
{ return (int)((ymax-y)/(ymax-ymin)*(getmaxy()+1));}
void triangle (float x1, float y1, float x2, float y2,
float x3, float y3, int color)
{
int z[6];
z[0]= ex(x1); z[1]= ey(y1); z[2]= ex(x2);
z[3]= ey(y2); z[4]= ex(x3); z[5]= ey(y3);
setfillstyle(SOLID_FILL, color); // setcolor(BLACK);
fillpoly(3, z);
}
void serp5k(float x1, float y1, float x2, float y2, float x3, float y3, int M, int color)
{
if (M>0)
{
serp5k(x1, y1, (x1+x2)/2, (y1+y2)/2, (x1+x3)/2,
(y1+y3)/2, M-1, color);
serp5k((x1+x2)/2, (y1+y2)/2, x2, y2, (x2+x3)/2,
(y2+y3)/2, M-1, color);
serp5k((x1+x3)/2, (y1+y3)/2, (x2+x3)/2, (y2+y3)/2,
x3, y3, M-1, color);
} else triangle (x1,y1,x2,y2,x3,y3,color);
}
main()
{
int gd=DETECT, gm;
initgraph(&gd,&gm,”C:\\PROGRAMM\\BC31\\BGI”);
setfillstyle(SOLID_FILL, WHITE);
bar(0, 0, getmaxx(), getmaxy());
setcolor(BLACK);
serp5k(0,0,1,0,0,1,4,BLACK);
getch();
closegraph();
return 0;
}
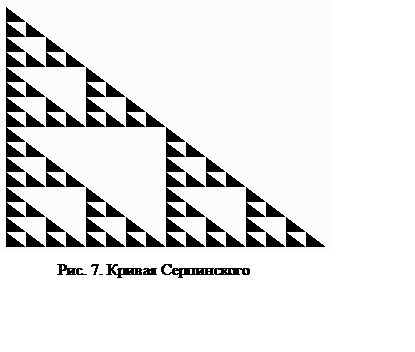
В главной программе подпрограмма, соответствующая процедуре,
описанной выше, вызывается для значения аргумента ![]() . В
результате на экран будет выведена фигура, полученная после четырех шагов (рис.
7)
. В
результате на экран будет выведена фигура, полученная после четырех шагов (рис.
7)
Вычислим размерность ![]() кривой
Серпинского. С этой целью разделим плоскость сетью прямых
кривой
Серпинского. С этой целью разделим плоскость сетью прямых 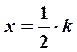 и
и 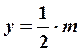 , где
, где ![]() и
и ![]() пробегают
целые числа. Плоскость будет разбита на квадраты со стороной
пробегают
целые числа. Плоскость будет разбита на квадраты со стороной 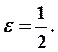
Поскольку 3 квадрата имеют общие точки с кривой Серпинского,
то 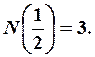 Затем разобьем плоскость сетью прямых
Затем разобьем плоскость сетью прямых 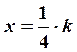 и
и 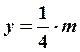 .
Получим
.
Получим 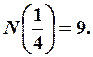 Повторяя разбиения для
Повторяя разбиения для 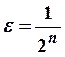 получим
получим 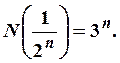 Следовательно,
Следовательно,
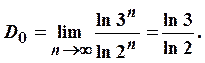
Системы итерируемых функций. Пусть ![]() - полное метрическое пространство,
- полное метрическое пространство, ![]() - конечное множество сжимающих отображений
- конечное множество сжимающих отображений ![]() в себя. В этом случае
в себя. В этом случае ![]() называется системой итерируемых функций
или
называется системой итерируемых функций
или ![]()
Пусть ![]() - ограниченное
замкнутое подмножество,
- ограниченное
замкнутое подмножество, ![]() - множество его
замкнутых подмножеств с метрикой Хаусдорфа. Тогда для произвольной системы итерируемых
функций
- множество его
замкнутых подмножеств с метрикой Хаусдорфа. Тогда для произвольной системы итерируемых
функций ![]() отображение
отображение ![]() ,
сопоставляющее каждому замкнутому подмножеству
,
сопоставляющее каждому замкнутому подмножеству ![]() множество
множество
![]() будет сжатием метрического пространства
будет сжатием метрического пространства ![]() относительно метрики Хаусдорфа.
относительно метрики Хаусдорфа.
Согласно принципу Банаха для сжатых
отображений, в силу полноты ![]() существует
единственное подмножество
существует
единственное подмножество ![]() такое, что
такое, что 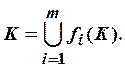 Это подмножество
Это подмножество ![]() называется
аттрактором или инвариантным множеством для
называется
аттрактором или инвариантным множеством для ![]() Аттрактор
Аттрактор ![]() для
для ![]() будет, как правило, фракталом. Его можно
вычислить как предел относительно метрики Хаусдорфа
будет, как правило, фракталом. Его можно
вычислить как предел относительно метрики Хаусдорфа ![]() , для
произвольного подмножества
, для
произвольного подмножества ![]()
Например, рассмотренный выше ковер Серпинского является аттрактором
системы, состоящей из восьми итерируемых функций, отображающих единичный
квадрат ![]() в себя.
в себя.
Кривая Серпинского также является аттрактором системы
итерируемых функций ![]() отображающих треугольник
отображающих треугольник ![]() в себя. Эти отображения для кривой
Серпинского определены следующим образом:
в себя. Эти отображения для кривой
Серпинского определены следующим образом:
![]()
![]()
![]()
Вычисление коэффициентов афинных преобразований.
Системы итерируемых функций могут состоять из афинных преобразований, которые
задаются с помощью ![]() матриц. Афинному преобразованию
матриц. Афинному преобразованию
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.