Методические указания к лабораторным работам по курсу “Компьютерная графика”, страница 4

·  Стохастические фракталы. Эти фракталы получаются в том случае, если в итерационном процессе случайным образом менять какие-либо его параметры. В качестве примера можно рассмотреть рекурсивную функцию изображения дерева, приведенную в учебном пособии «Компьютерная графика».

·  Системы итерируемых функций. Фрактал строится как множество, инвариантное относительно некоторых отображений плоскости в себя. Этот вид фракталов рассматривается в следующем параграфе.

Свойства размерности Хаусдорфа-Безиковича

·  Если  является открытым подмножеством, то .

·  Если  - непрерывно-дифференцируемое отображение открытого подмножества , в каждой точке которого ранг матрицы Якоби 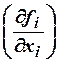 равен , то его образ  имеет размерность  Здесь  обозначают компоненты отображения , в том смысле, что для всех  верно равенство  В частности, гладкие кривые имеют размерность 1, гладкие поверхности имеют размерность 2.

·  Монотонность. Если , то

·  Размерность счетного объединения. Если  - подмножества евклидова пространства, то .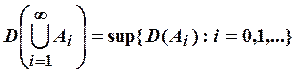

·  Для любого счетного множества  размерность  равна нулю.

·  Пусть  и  удовлетворяют условию Гельдера , при  Тогда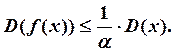

·  Отображение  называется липшицевым, если для некоторого числа  имеет место неравенство  при всех  Если сверх того, существует число  такое, что для всех  справедливы неравенства

то  называется би-липшицевым. Для липшицевых отображений верно неравенство  а для би-липшицевых – равенство

3. Системы итерируемых функций

Отображение  метрического пространства  в метрическое пространство  называется подобием, если существует число  такое, что для всех  имеет место равенство  Число  называется коэффициентом подобия.

Если  - биекция и подобие, то метрические пространства  и  называют подобными.

Самоподобные множества. Пусть  - подмножество евклидова пространства. Будем рассматривать его как метрическое пространство с метрикой 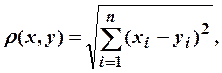 при  и  Ограниченное подмножество  евклидова пространства называется самоподобным, если  является объединением конечного числа попарно непересекающихся подмножеств, каждое из которых подобно .

Пример 7. Ковер Серпинского. Разобъем единичный квадрат на 9 частей, как это показано на рис. 5 и удалим квадрат, расположенный в центре. Затем эту процедуру применим к каждому из оставшихся восьми квадратов, получим 64 квадрата, к которым вновь применим эту процедуру и т.д. Приведем текст программы для вывода на экран фигуры, полученной через несколько шагов.

// ковер Серпинского, cover.cpp

#include <graphics.h>

#include <conio.h>

float xmin = -0.5, xmax = 1.5, ymin = -0.5, ymax = 1.5;

int ex(float x)

{

return (int)((x-xmin)/(xmax-xmin)*(getmaxx()+1));

}

int ey(float y)

{

return (int)((ymax-y)/(ymax-ymin)*(getmaxx()+1));

}

void square (float x0, float y0, float a, int color)

{

       setfillstyle(SOLID_FILL, color);

       bar(ex(x0), ey(y0+a), ex(x0+a), ey(y0));

}

void cover(float x0, float y0, float a, int M, int color)

{

int i,j;

if (M>0)

{

       for(i=0;i<3;i++)

             for(j=0;j<3;j++)

             {

                   if (!(i==1&&j==1))

                   cover(x0+i*a/3, y0+j*a/3, a/3, M-1, color);

}

} else square (x0, y0, a, color);

}

main()

{

int gd=DETECT, gm;

initgraph(&gd, &gm, “C:\\PROGRAMM\\BC31\\BGI”);

setfillstyle(SOLID_FILL, WHITE);

bar(0, 0, getmaxx(), getmaxy());

square(0, 0, 1, BLACK);

// setcolor(BLACK);

cover(0, 0, 1, 4, LIGHTGREEN);

getch();

closegraph();

return 0;

}

В результате работы программы будет выведена фигура, полученная через четыре шага.

После бесконечного числа шагов в пределе получится множество, состоящее из восьми подмножеств, содержащихся в квадратах, полученных после первого шага построения. Каждое из них будет подобно всему множеству с коэффициентом подобия 1/3, и они попарно не пересекаются.

Ящичная размерность. Для самоподобных множеств  размерность  Хаусдорфа-Безиковича равна ящичной размерности (box-counting dimension) , которая определяется следующим образом: