Отсюда вытекает, что если из ![]() -мерного
куба последовательно удалять открытые подмножества, то в результате получится
множество, равное пределу аппроксимирующих его множеств относительно метрики
Хаусдорфа.
-мерного
куба последовательно удалять открытые подмножества, то в результате получится
множество, равное пределу аппроксимирующих его множеств относительно метрики
Хаусдорфа.
Б. Мандельброт ввел следующее определение фрактала. Каждому
подмножеству ![]() -мерного евклидова пространства ставятся в
соответствие два числа – топологическая размерность
-мерного евклидова пространства ставятся в
соответствие два числа – топологическая размерность ![]() и размерность Хаусдорфа-Безиковича
и размерность Хаусдорфа-Безиковича
![]() . Топологическая размерность всегда целое
число. В общем случае имеет место
. Топологическая размерность всегда целое
число. В общем случае имеет место ![]() . Подмножество называется
фракталом или фрактальным множеством, если имеет
место строгое неравенство
. Подмножество называется
фракталом или фрактальным множеством, если имеет
место строгое неравенство ![]() . Цель данного параграфа
– дать опрделение размерностей
. Цель данного параграфа
– дать опрделение размерностей ![]() и
и ![]() .
.
 Перегородки и топологическая размерность. Пусть
Перегородки и топологическая размерность. Пусть ![]() - метрическое пространство. Каждое его
подмножество
- метрическое пространство. Каждое его
подмножество ![]() является метрическим пространством
относительно метрики
является метрическим пространством
относительно метрики ![]() . Замкнутое подмножество
. Замкнутое подмножество ![]() называется перегородкой в
называется перегородкой в ![]() , если
, если ![]() для
некоторых непустых непересекающихся открытых подмножеств
для
некоторых непустых непересекающихся открытых подмножеств ![]() . Если при этом
. Если при этом ![]() и
и ![]() , то
, то ![]() называется
перегородкой между
называется
перегородкой между ![]() и
и ![]() . На
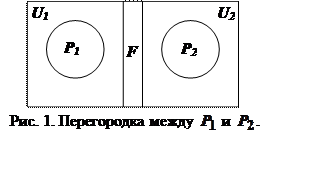
рис. 1 перегородка изображена в виде замкнутого прямоугольника,
. На
рис. 1 перегородка изображена в виде замкнутого прямоугольника, ![]() является большим замкнутым прямоугольником,
разбитым на прямоугольники
является большим замкнутым прямоугольником,
разбитым на прямоугольники ![]() ,
, ![]() и
и ![]() (подмножества
(подмножества
![]() и
и ![]() не
содержат общих с множеством
не
содержат общих с множеством ![]() граничных точек).
граничных точек).
Введем определение большой индуктивной
размерности. Она, по теореме Катетова, для метрических пространств совпадает с
размерностью Лебега и будет называться далее топологической размерностью.
Положим ![]() . При непустом
. При непустом ![]() полагаем
полагаем
![]() , если между любыми двумя непересающимися
замкнутыми подмножествами
, если между любыми двумя непересающимися
замкнутыми подмножествами ![]() и
и ![]() из
из ![]() найдется
перегородка
найдется
перегородка ![]() , для которой
, для которой ![]() Если
таких
Если
таких ![]() нет, то полагаем
нет, то полагаем ![]()
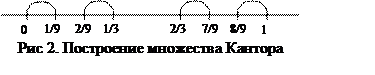 Пример 4. Множество
Кантора. Рассмотрим отрезок числовой прямой, состоящий из чисел
Пример 4. Множество
Кантора. Рассмотрим отрезок числовой прямой, состоящий из чисел ![]() , удовлетворяющих условиям
, удовлетворяющих условиям ![]() . Удалим среднюю часть отрезка, состоящую
из чисел
. Удалим среднюю часть отрезка, состоящую
из чисел ![]() , для которых
, для которых ![]() (рис. 2.).
Затем эту процедуру применим к каждому из двух оставшихся отрезков.
(рис. 2.).
Затем эту процедуру применим к каждому из двух оставшихся отрезков.
Затем удалим среднюю часть из каждого
из оставшихся множеств и т.д. Полученное в пределе множество называется множеством
Кантора С. Точки множества Кантора можно описать также как числа,
запись которых в троичной системе счисления ![]() состоит
из цифр
состоит
из цифр ![]() равных нулю или двум.
равных нулю или двум.
Такие числа можно записать как суммы рядов ![]() где
где ![]() Можно
доказать, что
Можно
доказать, что ![]()
Рассмотрим декартово произведение множества Кантора на себя,
![]() Оно состоит из точек плоскости
Оно состоит из точек плоскости ![]() таких, что
таких, что ![]() и
и ![]() . Из общего неравенства
. Из общего неравенства ![]() вытекает, что
вытекает, что ![]()
Размерность Хаусдорфа-Безиковича. Пусть ![]() - метрическое пространство,
- метрическое пространство, ![]() -подмножество,
-подмножество, ![]() - положительное
действительное число. Семейство
- положительное
действительное число. Семейство ![]() подмножеств
подмножеств ![]() называется
называется ![]() -покрытием,
если
-покрытием,
если ![]() для всех
для всех ![]() , и
, и 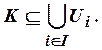 Для произвольного числа
Для произвольного числа ![]() определим число
определим число ![]() ,
где нижняя грань
,
где нижняя грань ![]() берется по всем
берется по всем ![]() -покрытиям множества
-покрытиям множества ![]() , у которых множество
, у которых множество ![]() счетно. Положим
счетно. Положим ![]() Размерность
Хаусдорфа-Безиковича, или фрактальная размерность,
определяется как верхняя грань чисел
Размерность
Хаусдорфа-Безиковича, или фрактальная размерность,
определяется как верхняя грань чисел ![]() , для которых
, для которых ![]() и она будет равна нижней грани чисел
и она будет равна нижней грани чисел ![]() , удовлетворяющих равенству
, удовлетворяющих равенству ![]()
![]()
Пример 5. Вычислим
размерность множества Кантора С. При ![]() и
и ![]() будет верно равенство
будет верно равенство
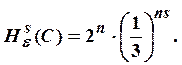
Следовательно, 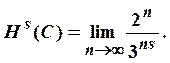 Этот предел при
Этот предел при 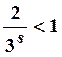 будет равен нулю, а в случае
будет равен нулю, а в случае 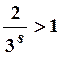 - бесконечен. Следовательно
- бесконечен. Следовательно ![]() равен числу
равен числу ![]() ,
удовлетсворяющему равенству
,
удовлетсворяющему равенству ![]() Получаем
Получаем 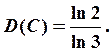 Поскольку
Поскольку ![]() то
то ![]() Отсюда вытекает, что множество Кантора
является фракталом. Аналогично можно вычислить размерность
Отсюда вытекает, что множество Кантора
является фракталом. Аналогично можно вычислить размерность ![]() .
.
Полагая ![]() при
при ![]() получаем
получаем 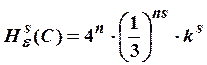 для некоторого
коэффициента
для некоторого
коэффициента ![]() Следовательно, для
Следовательно, для ![]() получаем
получаем
![]() Следовательно,
Следовательно, 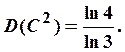
 На рис 3. изображено построение множества Кантора
На рис 3. изображено построение множества Кантора ![]() . Из единичного квадрата удаляется крест.
Затем этот процесс применяется рекурсивно к каждому из оставшихся квадратов.
. Из единичного квадрата удаляется крест.
Затем этот процесс применяется рекурсивно к каждому из оставшихся квадратов.
Черные квадраты состоят из точек, оставшихся после трех
шагов построения множества Кантора ![]() . Хорошо известно, что
между метрическими пространствами
. Хорошо известно, что
между метрическими пространствами ![]() и
и ![]() можно установить гомеоформизм. Поскольку
можно установить гомеоформизм. Поскольку ![]() и
и ![]() то
можно сделать вывод, что гомеоморфные геометрические фигуры могут иметь
различные размерности Хаусдорфа-Безиковича, следовательно, эта размерность не
является топологическим инвариантом.
то
можно сделать вывод, что гомеоморфные геометрические фигуры могут иметь
различные размерности Хаусдорфа-Безиковича, следовательно, эта размерность не
является топологическим инвариантом.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.