![]()
![]()
Для вывода фрактала на экран будем пробегать точки
треугольника ![]() и к каждой точке применять функции
и к каждой точке применять функции ![]() и
и ![]() ,
выбираемые случайным образом. Для выбора одной из функций генерируется число
,
выбираемые случайным образом. Для выбора одной из функций генерируется число ![]() из диапазона
из диапазона ![]() . Если
. Если ![]() меньше 60, что имеет место в
меньше 60, что имеет место в ![]() случаев, то применяется функция
случаев, то применяется функция ![]() , а в других случаях применяется функция
, а в других случаях применяется функция ![]() . Для наглядности изменяется цвет, в
зависимости от того, какая функция была выбрана. Общий цикл повторяется, пока
не нажата клавиша.
. Для наглядности изменяется цвет, в
зависимости от того, какая функция была выбрана. Общий цикл повторяется, пока
не нажата клавиша.
Программа
// стохастический метод изображения дракона Хартера-Хейтуэя dragst.cpp
#include <graphics.h>
#include <conio.h>
#include <stdlib.h>
#include <time.h>
float xmin = -0.5, xmax = 2.,
ymin = -0.5, ymax = 1.; // координаты окна
int ex(float x)
{ // экранная x-координата
return (int)((x-xmin)/(xmax-xmin)*(getmaxx()+1));
}
int ey(float y)
{ // экранная y-координата
return (int)((ymax-y)/(ymax-ymin)*(getmaxy()+1));
}
float f1x(float x, float y)
{
return(x+y)/2; // преобразование абсциссы первой функцией IFS
}
float f1y(float x, float y)
{
return(x-y)/2; // преобразование ординаты первой функцией IFS
}
float f2x(float x, float y)
{
return(x+y+1.)/2; // преобразование абсциссы второй функцией IFS
}
float f2y(float x, float y)
{
return(-x+y+1.)/2; // преобразование ординаты второй функцией IFS
}
main()
{
int gd=DETECT, gm; // драйвер видеоадаптера и номер режима
initgraph(&gd,&gm,”..\\BGI”); // инициализация графического режима
double x, y, xx, yy, xxx, yyy; // координаты точек
double hx=0.01, hy=0.01; // приращения координат
int i, M=100, k, cl; // счетчик, число итераций, случайное число, цвет
setfillstyle(SOLID_FILL, WHITE); // закраска экрана
bar(0,0,getmaxx(), getmaxy()); // белым цветом
randomize(); // инициализация генератора случайных чисел
while(!kbhit()) // пока не нажата клавиша
{
for (y=0.5; y>=0; y-=hy) // (x,y) пробегает точки треугольника
for(x=y; x<=1.-y; x+=hx) // с вершинами (0,0),(1,0),(0.5,0.5)
{
xx=x; yy=y;
for (i=0; i<M;i++) // итерация системы преобразований IFS
{
k=random(100);
if (k<60) // в 60% случаев
{ // применяется первое преобразование
xxx=f1x(xx,yy); yyy=f1y(xx,yy);
xx=xxx; yy=yyy; cl=BLUE;
} else // в остальных случаях
{ // применяется второе преобразование
xxx=f2x(xx,yy); yyy=f2y(xx,yy);
xx=xxx; yy=yyy; cl=GREEN;
}
} putpixel(ex(xx),ey(yy),cl); // вывод точки
}
} getch(); // прием симола с клавиатуры
closegraph(); return 0;
}
Результат работы программы

В данном параграфе будут рассмотрены инвариантные множества комплексных функций, отображающих плоскость в плоскость.
Множества Жюлиа. Пусть ![]() -
полином степени
-
полином степени ![]() с комплексными коэффициентами.
Будем рассматривать итерации отображения
с комплексными коэффициентами.
Будем рассматривать итерации отображения ![]() ,
применяемые к точкам плоскости
,
применяемые к точкам плоскости ![]() , определенные по
формуле
, определенные по
формуле ![]() , где
, где ![]() . Заметим,
что рассмотренные ниже понятия могут быть определены и исследованы для функций
. Заметим,
что рассмотренные ниже понятия могут быть определены и исследованы для функций ![]() , мероморфных в комплексной
плоскости (т.е. аналитичных во всех точках расширенной комплексной плоскости
, мероморфных в комплексной
плоскости (т.е. аналитичных во всех точках расширенной комплексной плоскости ![]() за исключением конечного числа полюсов).
Обозначим через
за исключением конечного числа полюсов).
Обозначим через ![]() -
- ![]() -ю
итерацию функции
-ю
итерацию функции ![]() ,
, ![]() Если
Если ![]() , то точка
, то точка ![]() называется
неподвижной точкой функции
называется
неподвижной точкой функции ![]() .
Если для некоторой точки
.
Если для некоторой точки ![]() и целого числа
и целого числа ![]() имеет место равенство
имеет место равенство ![]() , то точка
, то точка ![]() называется
периодической точкой функции
называется
периодической точкой функции ![]() . В этом
случае наименьшее целое число
. В этом
случае наименьшее целое число ![]() , для которого верно это
равенство, называется периодом точки
, для которого верно это
равенство, называется периодом точки ![]() , а множество
точек
, а множество
точек ![]() - орбитой периода
- орбитой периода ![]()
Для произвольной точки ![]() периода
периода
![]() обозначим
обозначим 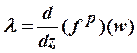 -
значение производной от функции
-
значение производной от функции ![]() в точке
в точке ![]() . Если
. Если ![]() , то
будем называть точку
, то
будем называть точку ![]() периода
периода ![]() притягивающей,
если
притягивающей,
если ![]() - индифферентной, если
- индифферентной, если ![]() - отталкивающей.
- отталкивающей.
Множеством Жюлиа ![]() функции
функции
![]() называется замыкание множества отталкивающих
периодических точек функции
называется замыкание множества отталкивающих
периодических точек функции ![]() . В случае, когда
. В случае, когда ![]() является полиномом, множество
является полиномом, множество ![]() является инвариантным множеством как для
отображения
является инвариантным множеством как для
отображения ![]() , так и для обратного отображения
, так и для обратного отображения ![]() Это множество непусто, ограничено и
замкнуто.
Это множество непусто, ограничено и
замкнуто.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.