![]() ,
,
![]()
будет соответствовать матрица
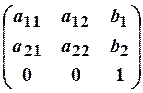 , определяющая в свою очередь линейное
преобразование трехмерного пространства, в котором точки плоскости будут
состоять из столбцов, являющихся тройками чисел
, определяющая в свою очередь линейное
преобразование трехмерного пространства, в котором точки плоскости будут
состоять из столбцов, являющихся тройками чисел ![]() . Если в
плоскости афинное преобразование
. Если в
плоскости афинное преобразование ![]() переводит треугольник,
вершины которого заданы радиус-векторами
переводит треугольник,
вершины которого заданы радиус-векторами ![]() , в
треугольник
, в
треугольник ![]() , то, добавляя к координатам точек третью
координату, равную 1, получим
, то, добавляя к координатам точек третью
координату, равную 1, получим ![]() матрицы
матрицы ![]() и
и ![]() ,
столбцами которых являеются координаты векторов с добавленными единицами.
Равенство произведения матриц
,
столбцами которых являеются координаты векторов с добавленными единицами.
Равенство произведения матриц ![]() матрице
матрице ![]() дает формулы для вычисления коэффициентов
афинного преобразования
дает формулы для вычисления коэффициентов
афинного преобразования ![]()
 Пример 9. Дракон
Леви. Пусть афинное преобразование
Пример 9. Дракон
Леви. Пусть афинное преобразование ![]() является
вращением вокруг начала координат против часовой стрелки на
является
вращением вокруг начала координат против часовой стрелки на ![]() , а
, а ![]() -
вращением по часовой стрелке вокруг точки
-
вращением по часовой стрелке вокруг точки ![]() .
Вычислим матрицы
.
Вычислим матрицы ![]() и
и ![]() этих
афинных преобразований. С этой целью рассмотрим треугольник с вершинами
этих
афинных преобразований. С этой целью рассмотрим треугольник с вершинами ![]() ,
, ![]() ,
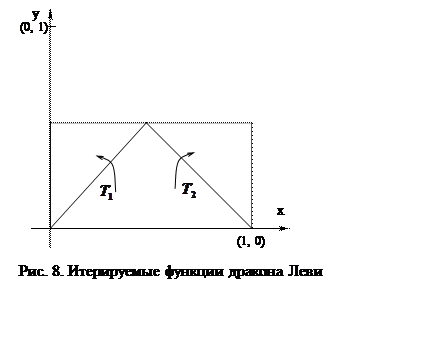
, ![]() (рис. 8). Преобразование
(рис. 8). Преобразование ![]() переводит его в треугольник, имеющий вершины
переводит его в треугольник, имеющий вершины
![]() ,
, ![]() и
и ![]() , а
, а ![]() -
- ![]() ,
, ![]() и
и ![]()
Поскольку в данном случае
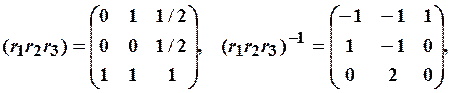
то получаем
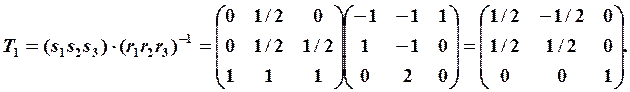
Аналогично,
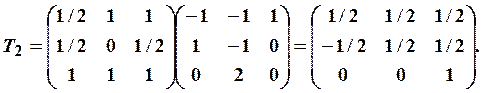
Следовательно,
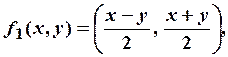
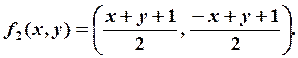
Подпрограмму, аппроксимирующую дракон Леви, реализуем с
помощью рекурсии. Если подставить в ней другие функции ![]() и
и
![]() , то получим подпрограмму, строящую фрактал
по другой системе итерируемых функций. Приведем текст подпрограммы и главной
программы для вывода дракона Леви.
, то получим подпрограмму, строящую фрактал
по другой системе итерируемых функций. Приведем текст подпрограммы и главной
программы для вывода дракона Леви.
//Дракон Леви DRAGON.CPP
#include <graphics.h>
#include <conio.h>
float xmin = -1, xmax = 2, ymin = -1, ymax = 1.5;
int ex(float x)
{
return (int)((x-xmin)/(xmax-xmin)*(getmaxx()+1));
}
int ey(float y)
{
return (int)((ymax-y)/(ymax-ymin)*(getmaxy()+1));
}
float f1x(float x, float y)
{
return (x-y)/2; // DXX (x+y)/2
}
float f1y(float x, float y)
{
return (x+y)/2; // DXX (x-y)/2
}
float f2x(float x, float y)
{
return (x+y+1.)/2;
}
float f2y(float x, float y)
{
return (-x+y+1.)/2;
}
void triangle (float x1, float y1, float x2, float y2,
float x3, float y3, int color)
{
int z[6];
z[0]= ex(x1); z[1]= ey(y1);
z[2]= ex(x2); z[3]= ey(y2);
z[4]= ex(x3); z[5]= ey(y3);
setfillstyle(SOLID_FILL, color);
fillpoly(3, z);
}
void dragon(float x1, float y1, float x2, float y2,
float x3, float y3, int M, int color)
{
if (M>0)
{
dragon(f1x(x1,y1), f1y(x1,y1),
f1x(x2,y2), f1y(x2,y2),
f1x(x3,y3), f1y(x3,y3),
M-1, color);
dragon(f2x(x1,y1), f2y(x1,y1),
f2x(x2,y2), f2y(x2,y2),
f2x(x3,y3), f2y(x3,y3),
M-1, color);
} else triangle (x1,y1,x2,y2,x3,y3,color);
}
main()
{
int gd=DETECT, gm;
initgraph(&gd, &gm, “C:\\PROGRAMM\\BC31\\BGI”);
setfillstyle(SOLID_FILL, WHITE);
dragon(0,0,1,0,0.5,0.5,15,15);
getch();
closegraph();
return 0;
}
Результат работы программы

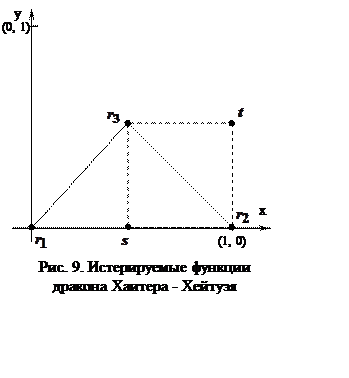 Стохастический метод изображения фракталов.
Рекурсивные подпрограммы, содержащие по крайней мере два обращения к себе,
обладают важным достоинством – такая реализация алгоритма позволяет
использовать параллельно выполняющиеся потоки. Тем не менее наиболее
существенный недостаток рекурсивных подпрограмм заключается в использовании
системного стека. Построение фракталов с большой точностью приводит к
переполнению стека. Описываемый далее метод вывода фракталов, заданных с
помощью систем итерируемых функций
Стохастический метод изображения фракталов.
Рекурсивные подпрограммы, содержащие по крайней мере два обращения к себе,
обладают важным достоинством – такая реализация алгоритма позволяет
использовать параллельно выполняющиеся потоки. Тем не менее наиболее
существенный недостаток рекурсивных подпрограмм заключается в использовании
системного стека. Построение фракталов с большой точностью приводит к
переполнению стека. Описываемый далее метод вывода фракталов, заданных с
помощью систем итерируемых функций ![]() основан на том, что
точки начальной геометрической фигуры подвергаются композиции преобразований
основан на том, что
точки начальной геометрической фигуры подвергаются композиции преобразований ![]() Точки фрактала состоят из пределов
Точки фрактала состоят из пределов ![]() где
где ![]() пробегает
все точки начальной фигуры. Для получения
пробегает
все точки начальной фигуры. Для получения ![]() -го
приближения организуется цикл, на каждом шаге которого выбирается случайное
число
-го
приближения организуется цикл, на каждом шаге которого выбирается случайное
число ![]() из
из ![]() и
применяется преобразование
и
применяется преобразование ![]()
В приведенном ниже примере случайное число 1 выбирается с
вероятностью ![]() , а случайное число 2 – с вероятностью
, а случайное число 2 – с вероятностью ![]() .
.
Пример 10. Дракон
Хартера-Хейтуэя. Рассмотрим систему итерируемых функций ![]() первая из которых переводит треугольник
первая из которых переводит треугольник ![]() (рис. 9) в треугольник
(рис. 9) в треугольник ![]() , а вторая переводит
, а вторая переводит ![]() в
в ![]()
Пусть ![]() и
и ![]() -
- ![]() -матрицы,
соответствующие афинным преобразованиям
-матрицы,
соответствующие афинным преобразованиям ![]() и
и ![]() Матрица
Матрица ![]() была
вычислена в примере 9. Находим
была
вычислена в примере 9. Находим
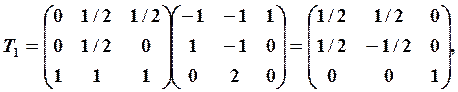
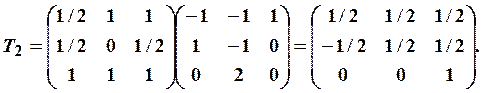
Получаем формулы для итерируемых функций:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.