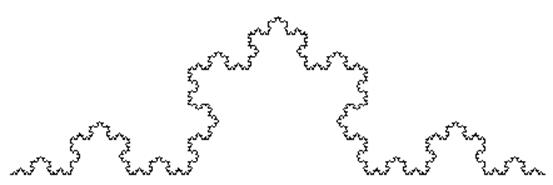
 Пример 6. Кривая Коха. Отрезок
разбивается на три равные части. Средняя часть удаляется и вместо нее
вставляется два отрезка, каждый из которых в три раза короче исходного. Затем
эта процедура применяется к каждому из четырех полученных отрезков (рис. 4.).
Затем это построение вновь применяется к каждому отрезку и т.д. Кривая,
получающаяся в пределе называется кривой Коха. Обозначим ее
Пример 6. Кривая Коха. Отрезок
разбивается на три равные части. Средняя часть удаляется и вместо нее
вставляется два отрезка, каждый из которых в три раза короче исходного. Затем
эта процедура применяется к каждому из четырех полученных отрезков (рис. 4.).
Затем это построение вновь применяется к каждому отрезку и т.д. Кривая,
получающаяся в пределе называется кривой Коха. Обозначим ее ![]() .
.
Приведем текст программы для изображения ломаной, полученной после многократной итерации этой процедуры.
//coh.cpp
#include <graphics.h>
#include <conio.h>
#include <stdlib.h>
#include <math.h>
float xmin = -1.5, xmax = 1.5, ymin = -0.7, ymax = 1.5; //координаты //окна
int ex(float x)
{ // экранная x-координата
return (int) ((x-xmin)/(xmax-xmin)*(getmaxx()+1));
}
int ey(float y)
{ // экранная y-координата
return (int) ((ymax-y)/(ymax-ymin)*(getmaxy()+1));
}
//функция построения кривой Коха
void coh(double xp, double yp, double xq, double yq, int M)
{
if (M>0)
{
coh(xp, yp, 2*xp/3+xq/3, 2*yp/3+yq/3, M-1);
coh(2*xp/3+xq/3, 2*yp/3+yq/3, xp/2+xq/2-(yq-yp)*sqrt(3)/6,
yp/2+yq/2+(xq-xp)*sqrt(3)/6, M-1);
coh(xp/2+xq/2-(yq-yp)*sqrt(3)/6, yp/2+yq/2+(xq-xp)*sqrt(3)/6,
xp/3+2*xq/3, yp/3+2*yq/3, M-1);
coh(xp/3+2*xq/3, yp/3+2*yq/3, xq, yq, M-1);
} else line (ex(xp), ey(yp), ex(xq), ey(yq));
}
main()
{
int gd=DETECT, gm; // драйвер виедоадаптера и номер режима
initgraph (&gd, &gm, “..\\BGI”); // инициализация графического режима
// setfillstyle(SOLID_FILL, WHITE); // закраска экрана
// bar(0,0,getmaxx(), getmaxy()); // белым цветом
coh(-1, 0, 1, 0, 5);
getch(); // прием символа с клавиатуры
closegraph(); return 0;
}
Результат работы программы:
Вычислим размерность Хаусдорфа-Безиковича кривой Коха. При 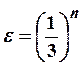 кривую можно покрыть выпуклыми множествами
кривую можно покрыть выпуклыми множествами
![]() диаметра
диаметра ![]() Число этих
множеств будет равно
Число этих
множеств будет равно ![]() Получаем
Получаем 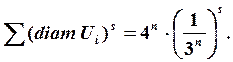 Предел
Предел
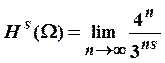 будет равен нулю при
будет равен нулю при 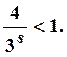 Нижняя грань чисел
Нижняя грань чисел ![]() ,
удовлетворяющих этому неравенству будет равна
,
удовлетворяющих этому неравенству будет равна 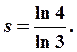 Следовательно,
Следовательно,
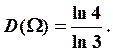
Классификация фракталов. Мы определили фрактал
как подмножество ![]() евклидова пространства,
удовлетворяющее неравенству
евклидова пространства,
удовлетворяющее неравенству ![]() Ниже приведена классификация
фракталов в зависимости от метода построения.
Ниже приведена классификация
фракталов в зависимости от метода построения.
· Геометрические фракталы. Эти фракталы самые наглядные. На плоскости их получают с помощью некоторой ломаной (в пространстве – с помощью поверхности), называемой генератором. Фрактал строится с помощью бесконечного повторения процедуры, состоящей в замене каждого отрезка генератором, как это делалось, например, при построении кривой Коха.
· Алгебраические
фракталы. Нелинейный процесс в ![]() -мерном
пространстве интерпретируется как дискретная динамическая система. Это
позволяет определять для нелинейных процессов понятия, аналогичные
рассматриваемым в теории динамических систем понятиям фазового портрета,
стационарного процесса, аттрактора и т.д. Нелинейные динамические системы
обладают несколькими устойчивыми состояниями. Эти устойчивые состояния
называются аттракторами (термин аттрактор применяется также и в
другом смысле, пп 3). Каждый аттрактор обладает некоторой областью начальных
состояний, из которых система обязательно попадет в состояние, соответствующее
этому аттрактору. Эта область называется областью притяжения данного аттрактора.
Если процесс происходит в плоскости, то окрашивая области притяжения различными
цветами, можно получить цветовой фазовый портрет этой системы. Рассмотрим, например,
множество Мандельброта, программа вывода которого на экран была приведена в
главе 2. Итерационный процесс описывается формулой
-мерном
пространстве интерпретируется как дискретная динамическая система. Это
позволяет определять для нелинейных процессов понятия, аналогичные
рассматриваемым в теории динамических систем понятиям фазового портрета,
стационарного процесса, аттрактора и т.д. Нелинейные динамические системы
обладают несколькими устойчивыми состояниями. Эти устойчивые состояния
называются аттракторами (термин аттрактор применяется также и в
другом смысле, пп 3). Каждый аттрактор обладает некоторой областью начальных
состояний, из которых система обязательно попадет в состояние, соответствующее
этому аттрактору. Эта область называется областью притяжения данного аттрактора.
Если процесс происходит в плоскости, то окрашивая области притяжения различными
цветами, можно получить цветовой фазовый портрет этой системы. Рассмотрим, например,
множество Мандельброта, программа вывода которого на экран была приведена в
главе 2. Итерационный процесс описывается формулой ![]() где
где ![]() и
и ![]() -
комплексные переменные. Итерация выполняется для каждой стартовой точки
-
комплексные переменные. Итерация выполняется для каждой стартовой точки ![]() прямоугольной области. Итерационный
процесс продолжается до тех пор, пока точка
прямоугольной области. Итерационный
процесс продолжается до тех пор, пока точка ![]() не
выйдет за пределы круга радиуса 2 с центром в точке
не
выйдет за пределы круга радиуса 2 с центром в точке ![]() Это
означает, что аттрактор динамической системы находится на бесконечности. Точка
может в течение достаточно большого числа итераций оставаться внутри круга, в
этом случае стартовая точка окрашивается в черный цвет. Если же точка
принадлежит области притяжения аттрактора, находящегося на бесконечности, то
она окрашивается в цвет, зависящий от числа итераций, при которых точка
оставалась в круге.
Это
означает, что аттрактор динамической системы находится на бесконечности. Точка
может в течение достаточно большого числа итераций оставаться внутри круга, в
этом случае стартовая точка окрашивается в черный цвет. Если же точка
принадлежит области притяжения аттрактора, находящегося на бесконечности, то
она окрашивается в цвет, зависящий от числа итераций, при которых точка
оставалась в круге.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.