Методические указания к лабораторным работам по курсу “Компьютерная графика”, страница 9

Легко видеть, что комплексная плоскость будет содержать области притяжения точек  и  относительно функции 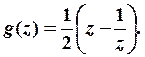 Область притяжения точки  состоит из точек с положительной ординатой - , а точки  - с отрицательной ординатой. Точки , для которых , будут составлять границу для каждой их этих областей.

В общем случае уравнение  решается с помощью итерации преобразования комплексной плоскости , где  производная в точке  Если  - полином степени , то комплексная плоскость будет содержать области притяжения корней этого уравнения. Границы этих областей называются фракталами Ньютона.

Рассмотрим, например, уравнение . Оно имеет корни: , , 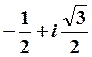 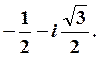Для изображения на экране компьютера областей притяжения этих точек относительно преобразования  в приведенной ниже программе пробегаются точки комплексной плоскости, пока значение  не станет достаточно малым. Затем исходные точки окрашиваются в цвета, соответствующие корням.

Текст программы

// newtcube.cpp

#include<graphics.h>

#include<stdio.h>

#include<conio.h>

#include<stdlib.h>

#include<complex.h>

#include<math.h>

#define MITER 100

double xmin=-1.5, ymin=-1, xmax=1.5, ymax=1;

int left=0, top=0, right=639, bottom=479;

int colors[6]={RED,LIGHTRED,GREEN,LIGHTGREEN,BLUE,LIGHTBLUE};

complex f(complex z)

{

   return z*z*z-1;

}

complex fs(complex z)

{

   return 3*z*z;

}

complex i(0.,1.);

complex root[3];

void putpoint (double x, double y, int color)

{

if(x<xmax&&x>xmin&&y<ymax&&y>ymin)

putpixel(left+(x-xmin)*(right-left)/(xmax-xmin),

        top+(ymax-y)*(bottom-top)/(ymax-ymin),color);

}

int main()

{

int gd=VGA, gm=VGAHI, j;

double re, im, xinc=(xmax-xmin)/640, yinc=(ymax-ymin)/480;

int pput, ncolors=0,n;

initgraph(&gd,&gm,"..\\BGI");

complex z;

 ncolors=3; root[0]=1.; root[1]= -0.5+i*sqrt(3.)/2; root[2]=-0.5-i*sqrt(3.)/2;

 for (re=xmin; re<xmax; re+=xinc)

  for (im=ymin; im<ymax; im+=yinc)

  {

     z=re+i*im; n=0;

     do

     {

      if (abs(fs(z))<0.0001) n=-1;

      else {z = z- f(z)/fs(z); n++;}

     } while ( n>=0&& n<MITER && abs(f(z))>=0.01);

     if (n<0) continue;

     for (j=0; j<ncolors; j++)

     {

      if (abs(z-root[j])<0.01)

 putpoint(re,im,colors[2*j+n%2]); //pput=1;

     }

  }

  getch(); closegraph();   return 0;

}

Область притяжения точки  будет выведена красным цветом, для точки 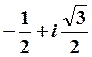 - зеленым, а для точки  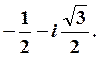- синим:

Результат работы программы:

Если указанная точность приближения корня достигнута через четное число шагов, то исходная точка окрашивается светлым, а если через нечетное, то темным цветом, соответствующим корню.

Более общий случай полинома  третьей степени будет рассмотрен как пример выполнения задания 2 из РГЗ2 («Интерактивные графические системы. Практика»). Там будет применен аналогичный метод построения областей притяжения корней.

Размерности алгебраических фракталов в настоящее время изучены не полностью. Многие работы посвящены вычислению и оценке размерностей этих фракталов. Разработаны алгоритмы и программы вычисления фрактальных размерностей. Размерность Хаусдорфа-Безиковича и другие фрактальные размерности ограничены сверху размерностью Булигана, которая определяется следующим образом:

·  пусть  - ограниченное подмножество (или, более общим образом, вполне ограниченное подмножество произвольного метрического пространства). Для каждого  обозначим через  наименьшее число множеств диаметра не превышающего , которым можно покрыть  Это число будет конечным для каждого , ибо  ограничено. Если  бесконечно, то  стремится к бесконечности при  Размерностью Булигана называется верхний предел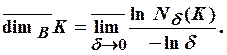

Пример 11. Для кривой Коха, получающейся из отрезка заменой его ломаной, начало и конец которой совпадают с вершинами отрезка, с последующей итерацией этой процедуры, как это описано в примере 6, значения  будут равны    …,  …. Следовательно, 

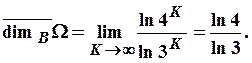
5. Варианты заданий к лабораторной работе